Exploring Thermoelectric Transport Properties and Band Parameters of n-Type Bi_2-xSb_xTe₃ Compounds Using the Single Parabolic Band Model

Article information

Abstract

1. Introduction

Thermoelectric (TE) technology directly converting waste heat into electricity holds significant promise in environmental protection [1, 2]. As the efficiency of thermal-to-electrical energy conversion relies heavily on TE materials, extensive research efforts have been devoted to enhancing TE performance and developing new materials over the past 60 years [3-6]. Bismuth telluride (Bi₂Te₃)-based materials, including (Bi,Sb)₂Te₃ for p-type and Bi₂(Te,Se)₃ for n-type, have long been recognized for their significant potential in commercial thermoelectric applications, owing to high TE conversion efficiency [7-9]. The materials’ TE performance is evaluated by a dimensionless figure of merit zT=S²σT/κ_tot (κ_e+κ_L), where S, σ, T, κ_tot, κ_e and κ_L are the Seebeck coefficient, electrical conductivity, absolute temperature, total thermal conductivity, electronic thermal conductivity, and lattice thermal conductivity, respectively [10] While zT value serves as a primary parameter, balancing between the p- and n-type materials also plays a pivotal role in determining the overall performance of a TE device [11]. Over the decades, efforts to improve zT of TE materials have led to notable advancements achieved through a diverse array of strategies including nanostructuring [12-14], lattice planification [15], carrier filtering [16, 17], resonant doping [18, 19], band convergence [20, 21] and so forth. However, the TE performance of n-type Bi₂(Te,Se)₃ compounds (with zT ~1.22 at 323K) [22] lags somewhat behind that of their counterpart p-type (Bi,Sb)₂Te₃ (with zT ~1.86 at 320K) [23], posing challenges in the development of high-performance TE devices and thereby limiting their practical applications.

The inferior TE performance of n-type Bi₂(Te,Se)₃ originates from intrinsically unfavorable electronic transport properties, such as high carrier concentration [24], strong dependence of carrier mobility on structural texturing [25], and single valley contribution to electrical properties of Bi₂Se₃ [26]. Recently, Zhou et al. developed a new n-type Bi_2-xSb_xTe₃, tackling the aforementioned issues in conventional n-type Bi₂(Te,Se)₃ [11]. It offers several advantages including optimized electron concentration, multi-valley contribution for high S, and larger mass differences for low κ, resulting in a high zT value of ~1.0 at 330 K for Bi_1.5Sb_0.5Te_3.0 even without applying strategies to enhance TE properties [11]. This highlights the possibility of further improving the zT of n-type Bi₂Te₃-based materials. In this regard, a comprehensive investigation into the TE transport properties and understanding of the electronic band structure of n-type Bi_2-xSb_xTe₃ is necessary as a preliminary study.

In this work, we investigated the temperature-dependent TE transport properties of n-type Bi_2-xSb_xTe₃ (x = 0.1 – 1.1) and characterized the band parameters using the single parabolic band (SPB) model. The calculated weighted mobility (μ_w) was found to be highest at x = 0.1 and decreased with increasing Sb content, indicating that lower Sb content led to more favorable electronic transport properties. Consequently, a maximum power factor (S²σ) of ~2.2 mW m^-1 K^-2 was observed at 300 K for x = 0.1. Meanwhile, the higher carrier concentration at lower x suppressed the bipolar contribution to the total thermal conductivity (κ_tot). As a result, the peak zT value for x = 0.1 was the highest, reaching ~ 0.5 at 450 K. Furthermore, SPB model-based estimation of Hall carrier concentration (n_H) dependent zT values suggests that the zT value for x = 0.1 could be improved by ~70% (from 0.3 to 0.5) through optimizing n_H at room temperature.

2. Experimental Procedure

Bi_2-xSb_xTe₃ (x = 0.1, 0.3, 0.5, 0.7, 0.9, 1.1) powders were synthesized via a ball-milling process. High-purity (~99.999%) Bi, Sb, and Te shots were used as raw materials. They were weighed according to the desired ratio to achieve stoichiometry and ball-milled using planetary mill (Pulverisette 5, Fritsch, Germany). The ball-milling process consisted of two steps: the first step operated at 360 rpm for 48 cycles, and the second step operated at the same speed for 24 cycles. The obtained powder was reduced in the H2 atmosphere at 573K in 90 min. Cylinder-type bulks (15 mm in diameter and 12 mm in thickness) were fabricated by using spark plasma sintering (SPS) at 753K for 5 min under 30, 40, and 50MPa. The crystalline phases of the ball-milled powders were identified using X-ray diffraction (XRD) with a Cu K_α1 X-ray source (Malvern Panalytical, United Kingdom). The temperature-dependent electrical conductivity and Seebeck coefficient were measured by SBA458 Nemesis (Netzsch, Germany) from 298K to 473K in an argon atmosphere. The Hall carrier concentration and Hall mobility were measured using the van der Pauw configuration with an HMS3500 (Ecopia, South Korea) at room temperature. The temperature-dependent thermal conductivity was determined using the equation of κ = DρC_p, where D, ρ and C_p are thermal diffusivity, density and specific heat. Thermal diffusivity was measured by laser flash method (NETZSCH, Germany) and the density was measured using Archimedes method. The specific heat was estimated by the corrected Dulong-Petit law [27, 28]. The electrical and thermal properties were measured along the direction perpendicular to the pressing direction of SPS.

3. Results and Discussion

Fig. 1(a) and Fig. 1(b) shows the X-ray diffraction (XRD) patterns of n-type Bi_2-xSb_xTe₃ (x = 0.1 – 1.1) ball-milled powders. The peaks are clearly indexed to Bi₂Te₃ (JCPDS #15-0863), indicating the synthesis of single phases of n-type Bi_2-xSb_xTe₃ (x = 0.1 – 1.1) across all compositions. The peaks shifted to higher angles with increasing x, suggesting the change in lattice parameters upon the substitution of Sb at Bi sites. As illustrated in Fig. 1(c), the calculated lattice parameter a gradually decreased with increasing Sb content, which can be attributed to the smaller atomic size of Sb compared to Bi (r_Sb = 1.45 Å, r_Bi = 1.60 Å). Meanwhile, it was observed that the lattice parameter c increased, likely due to the differences in electronegativity between Bi and Sb [11] These results suggest that the successful substitution of Sb atoms at the Bi site without the formation of any second phases.

Fig. 1.

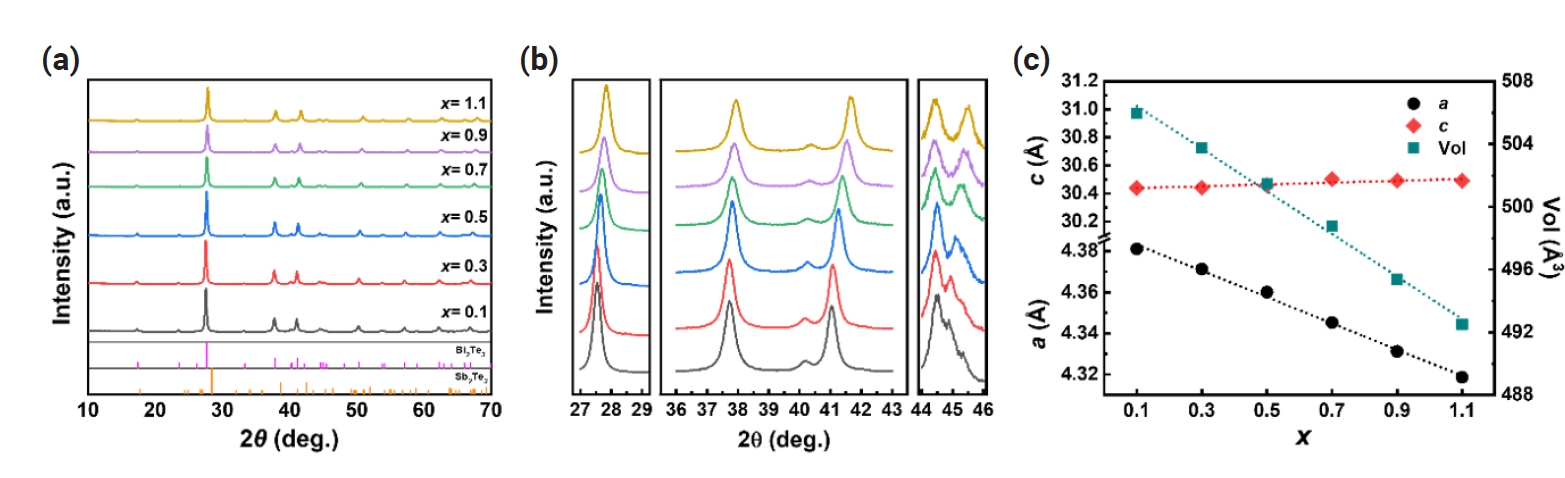
(a) X-ray diffraction (XRD) patterns and (b) three close-up views of (a) with the 2θ ranging between 27–29°, 36–43° and 44–46° (c) lattice parameters (a and c) and unit cell volume of n-type B_2-xSb_xTe₃ (x = 0.1 – 1.1).

Fig. 2 shows the electrical conductivity (σ), Seebeck coefficient (S), and power factor (S²σ) as a function of temperature for spark plasma sintered (SPSed) Bi_2-xSb_xTe₃ (x = 0.1 – 1.1). As shown in Fig. 2(a), Bi_1.9Sb_0.1Te₃ exhibited the highest σ at room temperature, ~1895 S cm^-1, and decreased with increasing temperature to ~1093 S cm^-1 at 473K. The σ of the Bi_2-xSb_xTe₃ compound gradually decreased as the x decreases due to the suppression of donor-like effect by excess Bi_Te antisites defect, with the lowest σ of ~237 S cm^-1 observed at room temperature for x = 1.1. The measured S values are negative, indicating n-type carrier transport behavior. The absolute value of S increased with increasing x from 108 μV K^-1 (x = 0.1) to 148 μV K^-1 (x = 1.1) at 300 K (Fig. 2b). Also, it is observed that the temperature at which the peak S value occurs shifted to higher temperatures with decreasing Sb content. The changes in σ and S can be ascribed to the trade-off relationship between σ and S, and the differences in temperature dependence of S with Sb content are due to the increased or reduced bipolar contribution at different x [29-33]. The power factor (S²σ) calculated from the measured σ and S exhibited the highest value of ~2.2 mW m^-1 K^-2 for x = 0.1 and gradually decreased with increasing x, and reaching ~0.5 mW m^-1 K^-2 for x = 1.1 at 300K (Fig. 2c).

Fig. 2.

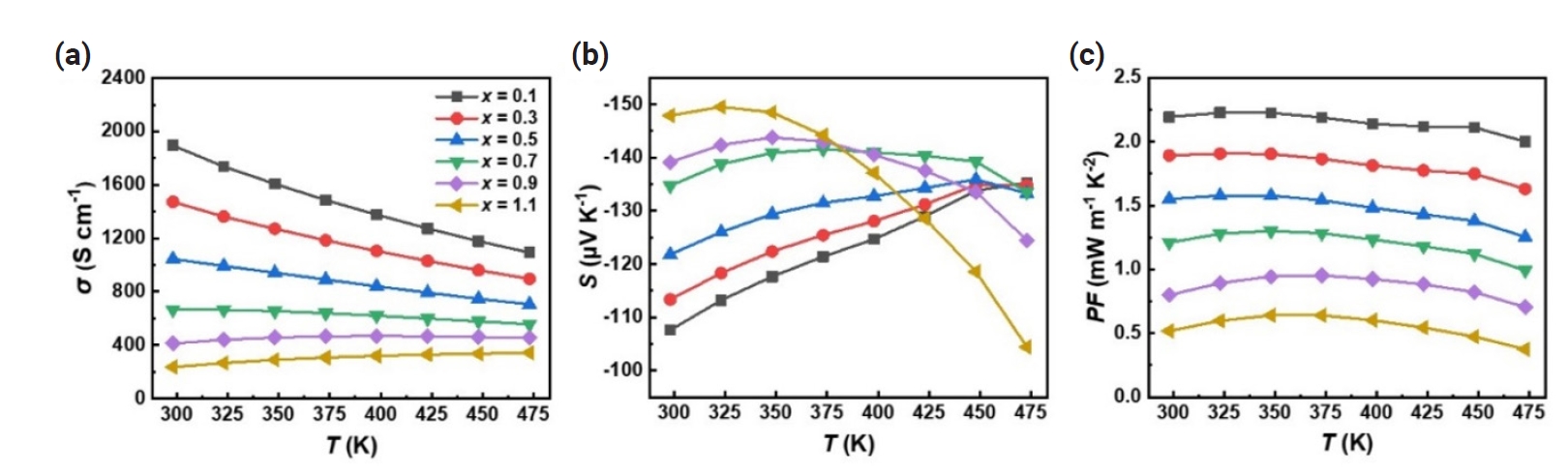
Temperature-dependent (a) electrical conductivity (σ), (b) Seebeck coefficient (S), and (c) power factor (S²σ) of spark plasma sintered (SPSed) Bi_2-xSb_xTe₃ (x = 0.1 – 1.1).

To understand the change in electrical properties, we measured the Hall carrier concentration (n_H) and Hall mobility (μ_H), as shown in Table 1. As expected, both n_H and μ_H gradually decreased with increasing x, which accounts for the decrease in σ and the increase in S with increasing Sb content. To gain a deeper understanding on the origin of differences in electronic transport properties of Bi_2-xSb_xTe₃ (x = 0.1 – 1.1), we estimated the density-of-state effective mass (m_d^*) and nondegenerate mobility (μ₀) using the single parabolic band (SPB) model. We obtained n_H dependent S (n_H-S) curve for a given m_d^* using the following equations and fitted them to the experimentally measured n_H and S (Fig 3a),

Table 1.

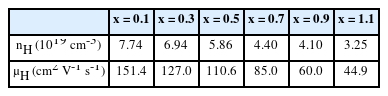
Hall carrier concentration (n_H) and Hall mobility (μ_H) of Bi_2-xSb_xTe₃ (x = 0.1 – 1.1) measured at room temperature

Fig. 3.

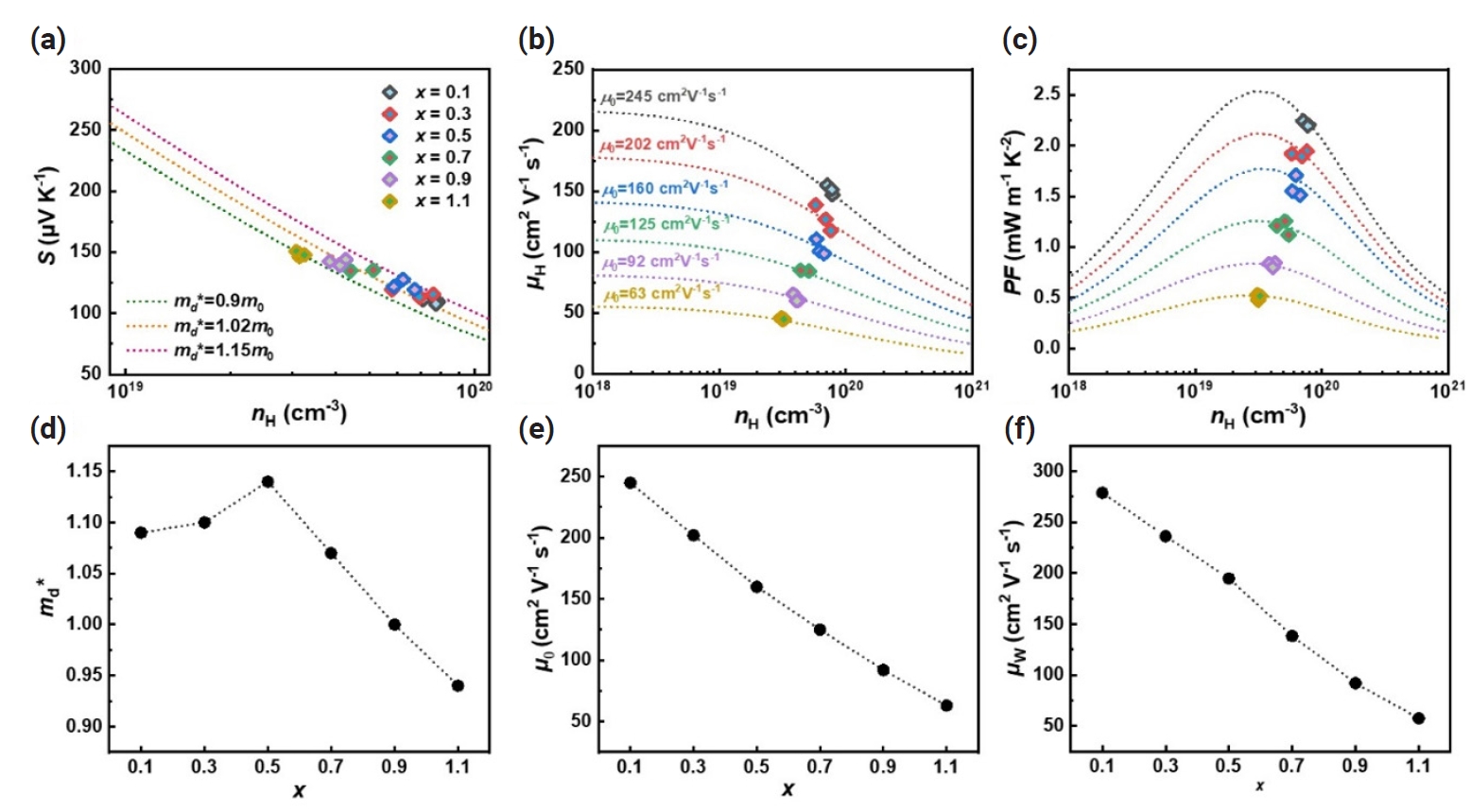
Hall carrier concentration (n_H) dependent (a) Seebeck coefficient (S), (b) Hall carrier mobility (μ_H), and (c) power factor (S²σ) of Bi_2-xSb_xTe₃ (x = 0.1 – 1.1). (d) density-of-state effective mass (m_d^*), (e) nondegenerate mobility (μ₀), and weighted mobility (μ_w) as a function of x. The single parabolic band (SPB) modeling was conducted using experimentally measured values at room temperature.

where k_B, e, F_j, η, and h are the Boltzmann constant, elemental electric charge, Fermi integral of order j, reduced Fermi energy, and Planck’s constant, respectively. The estimated values of m_d^* of Bi_2-xSb_xTe₃ (x = 0.1 – 1.1) range from ~0.9 for x = 1.1 to 1.15 m₀ for x = 0.5 where m₀ is the free electron mass (Fig. 3d). These variations in m_d^* could be attributed to changes in band curvature that occur with compositional changes [34]. In addition, we obtained n_H dependent μ_H (n_H-μ_H) curves for a given μ₀ using the following equations (Fig. 3b),

where C_l, m_b^* and E_def are the elastic constant, single band effective mass and deformation potential, respectively. The estimated μ₀ values range from ~245 cm² V^-1 s^-1 for x = 0.1 to 63 cm² V^-1 s^-1 for x = 1.1, showing a decreasing trend with increasing x (Fig. 3e). Given that μ₀ is inversely proportional to the m_b^*, it is reasonable that μ₀ decreased with increasing x up to x = 0.5. However, for x > 0.5, the m_d^* and μ₀ decreased simultaneously, which might be a result of the intensified carrier scattering induced by enhanced atomic disorder [35]. Fig. 3c shows the n_H-dependent power factor (n_H-S²σ) curve predicted by the SPB model, which agrees well with experimentally obtained S²σ at all compositions. Also, it is noted that with smaller x, n_H deviates more from the optimized value for maximum S²σ, suggesting that the electrical properties of Bi_2-xSb_xTe₃ (x = 0.1 – 1.1) can be improved by adjusting n_H. The weighted mobility (μ_w = μ₀ (m_d^*/m₀)^3/2) as a function of x was presented in Fig. 3(f), calculated using theoretically estimated m_d^* and μ₀ (Fig. 3f). The μ_w is the primary parameter for the electrical properties of a given material, as the maximum S²σ is in direct proportion to the μ_w [36]. As shown in Fig. 3(f), the calculated μ_w gradually decreases as x increases. Therefore, it is concluded that Bi_2-xSb_xTe₃ exhibits the most favorable electronic transport properties at x = 0.1 thanks to the optimized balance between m_d^* and μ₀.

The temperature-dependent thermal properties of Bi_2-xSb_xTe₃ (x = 0.1 – 1.1) are shown in Fig. 4. As x increases, the total thermal conductivity (κ_tot) decreases and the lowest κ_tot of ~1.02 W m^-1 K^-1 was observed at x = 1.1, which should be attributed to the reduced electronic contribution as we observed in Fig. 2(a). To further understand the changes in thermal properties, we calculated the lattice thermal conductivity (κ_L= κ_tot – κ_e) by subtracting the κ_e from the κ_tot. The κ_e was determined using the Wiedemann-Franz law (κ_e = L₀σT), where L₀ is the Lorenz number (in 10^-8 W Ω K^‒2). We determined L₀ using the following equation proposed by Kim et al [37].

Fig. 4.

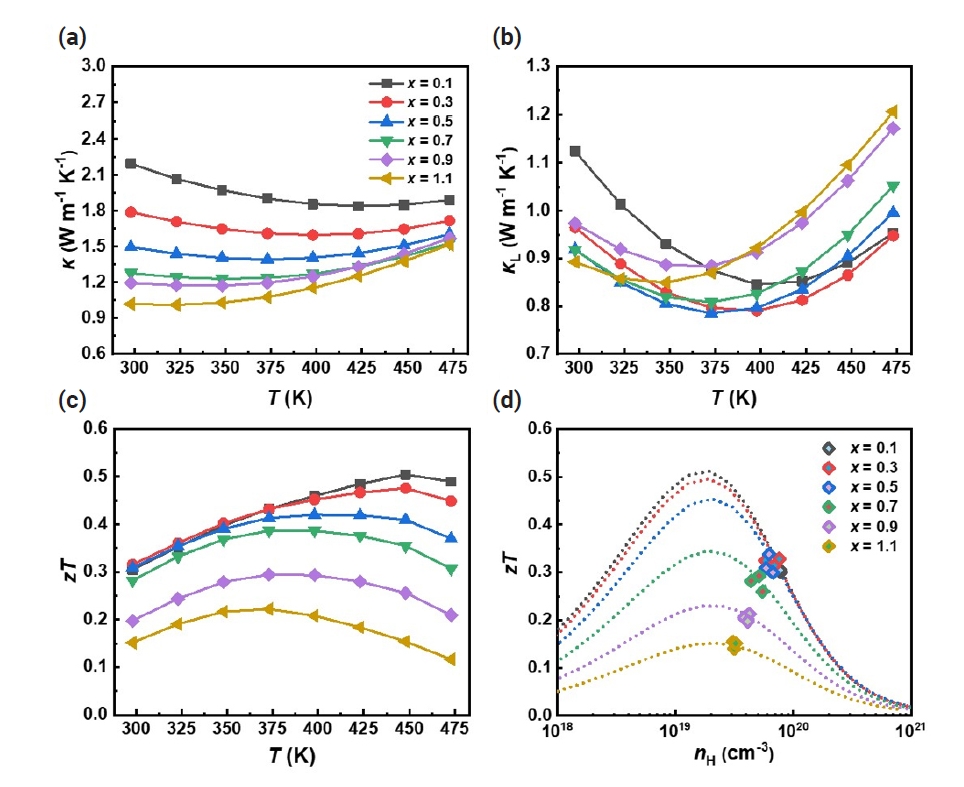
Temperature-dependent (a) total thermal conductivity (κ_tot), (b) lattice thermal conductivity (κ_L), and (c) figure of merit zT of Bi_2-xSb_xTe₃ (x = 0.1 – 1.1). (d) Hall carrier concentration (n_H) dependent zT (n_H-zT) curves were estimated at room temperature using the single parabolic band (SPB) model.

The κ_L exhibited a decreasing trend as the Sb content increased with the lowest κ_L of ~0.9 W m^-1 K^-1 observed at x = 1.1 (Fig. 4b). The reduction of κ_L with increasing x could be attributed to the intensified point defect scattering as discussed in Fig. 3 and indicated by the following equation [29],

where x is the doping fraction, ΔM/M is the rate of change of relative atomic mass, a_disorder and a_pure represent the lattice constants of disordered and pure alloys, and ε is an elasticity. It is also worth noting that κ_L decreased at elevated temperature with increasing x, suggesting the suppressed contribution of bipolar carriers due to increased n_H [33].

The temperature-dependent figure of merit zT was evaluated from the measured σ, S, and κ_tot (Fig. 4c). The maximum zT value of ~0.5 was observed at 450 K for the x = 0.1 sample and the zT values decreased with increasing x within the measured temperature ranges. Furthermore, we obtained the n_H-dependent zT (n_H-zT) curve using the SPB model (Fig. 4d), and it was found that the zT values predicted based on the SPB model agree well with the experimentally evaluated ones. It is noteworthy that n_H deviates more from the optimized value with lower Sb content (smaller x), indicating the need to optimize n_H at lower x to further improve zT. According to the SPB model, zT can be improved by up to ~70% (e.g., from ~0.3 to ~0.5 for x = 0.1) by tuning n_H at room temperature (Fig. 4d).

4. Conclusion

In this study, we investigated the thermoelectric properties and related band parameters of Bi_2-xSb_xTe₃ (x = 0.1 – 1.1) using both experimental and theoretical approaches. Our findings, based on the estimation of weighted mobility (μ_w), revealed that the electronic transport properties are most favorable for x = 0.1, attributed to the balanced density-of-state effective mass (m_d^*) and nondegenerate mobility (μ₀). Additionally, at lower Sb content, the bipolar contribution to thermal conductivity is reduced at elevated temperatures. These synergetic effects led to the highest zT value of ~0.5 at 450 K in Bi_1.9Sb_0.1Te₃. Furthermore, theoretical predictions by the single parabolic band (SPB) model suggest that the zT values can be further improved by up to ~70% through manipulating the carrier density. We believe that the current study not only contributes to the basic understanding of the n-type Bi_2-xSb_xTe₃ but also expedites the development of high-performance n-type Bi₂Te₃-based thermoelectric materials.

Article information Continued