Machine Learning Modeling of the Mechanical Properties of Al2024-B4C Composites
Article information
Abstract
Aluminum-based composites are in high demand in industrial fields due to their light weight, high electrical conductivity, and corrosion resistance. Due to its unique advantages for composite fabrication, powder metallurgy is a crucial player in meeting this demand. However, the size and weight fraction of the reinforcement significantly influence the components' quality and performance. Understanding the correlation of these variables is crucial for building high-quality components. This study, therefore, investigated the correlations among various parameters—namely, milling time, reinforcement ratio, and size—that affect the composite’s physical and mechanical properties. An artificial neural network model was developed and showed the ability to correlate the processing parameters with the density, hardness, and tensile strength of Al2024-B4C composites. The predicted index of relative importance suggests that the milling time has the most substantial effect on fabricated components. This practical insight can be directly applied in the fabrication of high-quality Al2024-B4C composites.
1. Introduction
Aluminum alloys have wide applications due to their lightweight, high electric conductivity and corrosion resistance. However, they have limited applications due to their low stiffness, resistance to wear and tear, and low yield strength. The industry demands advanced materials and technology to prepare these materials, including aerospace, automotive sectors, and defense [1]. Meanwhile, metal matrix composites (MMC) based on aluminum alloys provide superior properties such as increased specific strength and stiffness, improved properties at high temperatures, lower thermal expansion, and better wear resistance [2]. It has been investigated that adding ceramic particles to aluminum improves its strength, wear, and corrosion resistance [3]. Various fabrication techniques have been explored for MMC. These include powder metallurgy, molten metal methods, semi-solid casting, pressure infiltration, and spray deposition. The powder metallurgy processing technique is attractive for several reasons. This method offers microstructural control of the phases absent from the various routes involving a liquid phase. The powder metallurgy processing employs lower temperatures and reduced diffusion rates with better control of interface reaction kinetics [4]. Due to these reasons, the undesired phases between the matrix and reinforcement phases are eliminated, and the reinforcement particles are well distributed in the matrix [5].
Regarding powder production, the Al metal powder can be prepared using physical, chemical, and mechanical methods. The gas atomization process has been widely employed as an effective method to produce fine spherical metal powders. In brief, the principle of high-pressure gas atomization is to transfer kinetic energy from a high-speed gas jet to a liquid metal stream. The liquid metal stream becomes destabilized and breaks into successively atomized ligaments. In this process, the produced particles undergo in–flight solidification and are collected as a metal powder [6]. For the production of metal matrix composites (MMC), the mechanical milling technique can help to achieve the homogeneous mixing of ceramic reinforcement particles with the matrix materials [7]. In general, Al-based MMC composites are mainly reinforced with SiC and Al2O3.
Moreover, various studies investigated the possibility of adding other materials, such as TiC, VC, AlN, and Si3N4, in aluminum MMC through mechanical milling [8]. In particular, the boron carbide (B4C) reinforcement was used to develop various composite materials with enhanced properties [9]. Among the various ceramic reinforcements, the B4C is an ideal candidate due to its high strength and hardness, low coefficient of thermal expansion (CTE), excellent wear resistance, low density (2.51 g/cm3), high melting point (2450°C), good chemical resistance and relatively low cost. Thus, B4C reinforced Al composites are of significant importance in various fields of application, especially in the nuclear industry.
The mechanical performance of these MMCs depends on the processing parameters during production. The relationship between process parameters and physical and mechanical properties is complex and non-linear. We developed an artificial neural network (ANN) to understand this complex relation better. ANN is a computational model that has been used in many materials-related issues. The advantage of the ANN model is not limited to correlating the non-linear variables but also providing the optimum set of input variables to get the desired output. ANN model can process complex input-output relationships without any help of explicit mathematical models and is getting attention in materials science and engineering to solve complex problems unsuitable for traditional methods [10, 11]. ANN contains much information and imitates biological systems regarding learning ability. This allows the researcher to develop a potential predictive model, as conventional models are sometimes lacking because of theoretical complexity. Many networks have been created, but backpropagation neural networks are most widely used in which data are forward-fed into the network without feedback [12]. In the present study, we focused on developing the ANN model by using experimental data sets to investigate the influence of process parameters on the B4C-reinforced aluminum composite's hardness, strength, and density.
2. Materials and methods
2.1. Data collection and input-output variables of the model
ANN model is a biologically inspired computation program designed to simulate various non-linear and complex problems across multiple research fields [13-16]. ANN contains neurons connected with coefficients called weights. Each neuron connects to the other and forms a neural network; the power of neurons comes from the weights of the connections in the network [16]. ANN model gathers their knowledge by detecting the relationship between experimental datasets; this phenomenon is called training and testing of the model. The model accuracy depends on the minimum error in prediction during training. The present model utilizes the 33 experimental datasets, in which 25 were used for training, and eight were used for testing the ANN model, data collected from the published literature [7]. All the input and output variables were normalized between 0.1 and 0.9 using the following equation [17].
Where xn is the normalized value of x, xmax and xmin are the maximum and minimum values of x, respectively, in the whole data sets. After training the model, all the data sets were put back in the following equation [17].
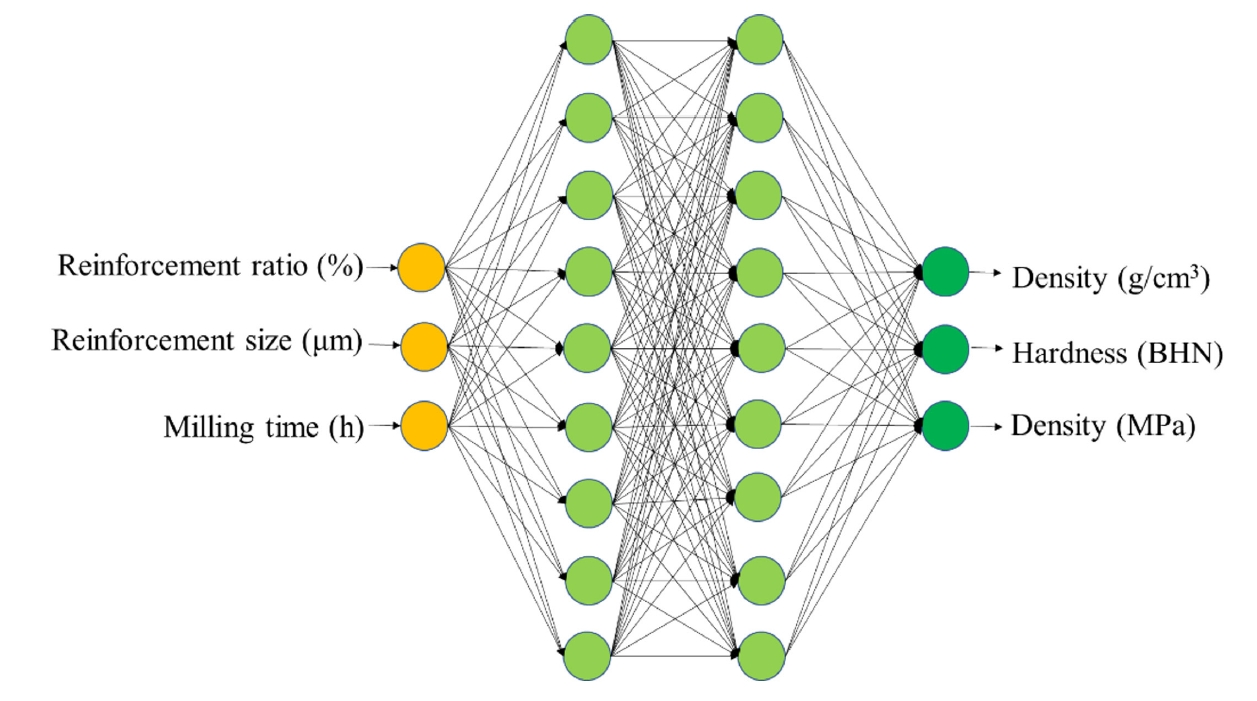
Three input process parameters, such as reinforcement volume (%), reinforcement size (μm), and milling time (h), are used in the developed model, whereas density (g/cm3), hardness (BHN), and tensile strength (MPa) are used as output parameters.
2.2. Training procedure of ANN model
The model training procedure is shown in our previous study [17]. Training is updating an internal representation of an external system in such neural systems. The present ANN model is trained with the backpropagation algorithm with a sigmoid activation function [13]. The backpropagation algorithm and its implementation have been explained in the literature [18-20]. The training program and graphical user interface were designed in C and Java. The training of the model is accompanied by the minimum difference in predicted and experimental density (g/cm3), hardness (BHN), and tensile strength (MPa). The total data sets are divided into training and testing data sets. The training data sets are used for the development of the model, whereas the testing data sets are used for the validation of the model. The model hyperparameters, such as the number of hidden layers, neurons in the hidden layers, momentum term, learning rate, and the number of iterations, were optimized to get the optimum model structure [21, 22]. These hyperparameters were selected based on the minimum root mean square error (RMSE) and minimum average deviation in output prediction (MAEr) of the test data as given in the following equations:
Where MAE is the average error in the prediction of testing data sets for output parameters y, N = number of data sets, Ti (y)= target output, Oi (y) = calculated output.
The optimum number architecture of the ANN model was obtained by testing with a single hidden layer and two hidden layers [17]. In the initial case, the model was trained with one hidden layer with momentum term 0.8, learning rate 0.7, and iterations of 90000 with hidden neurons varying from 2 to 9. The optimal model architecture with two hidden layers and nine hidden neurons (with an MAE of 3.48) is illustrated in Fig. 1.
3. Result and discussion
3.1. Validation of ANN model and weights distribution
The developed model performance was evaluated by measuring Pearson's r and Adj. R2 values between experimental and predicted output values (Fig. 2). The correlation coefficient values between experimental and predicted hardness (BHN) are nearly 100% for train and test datasets. This indicates that the model prediction is comparably favored with experimental data.
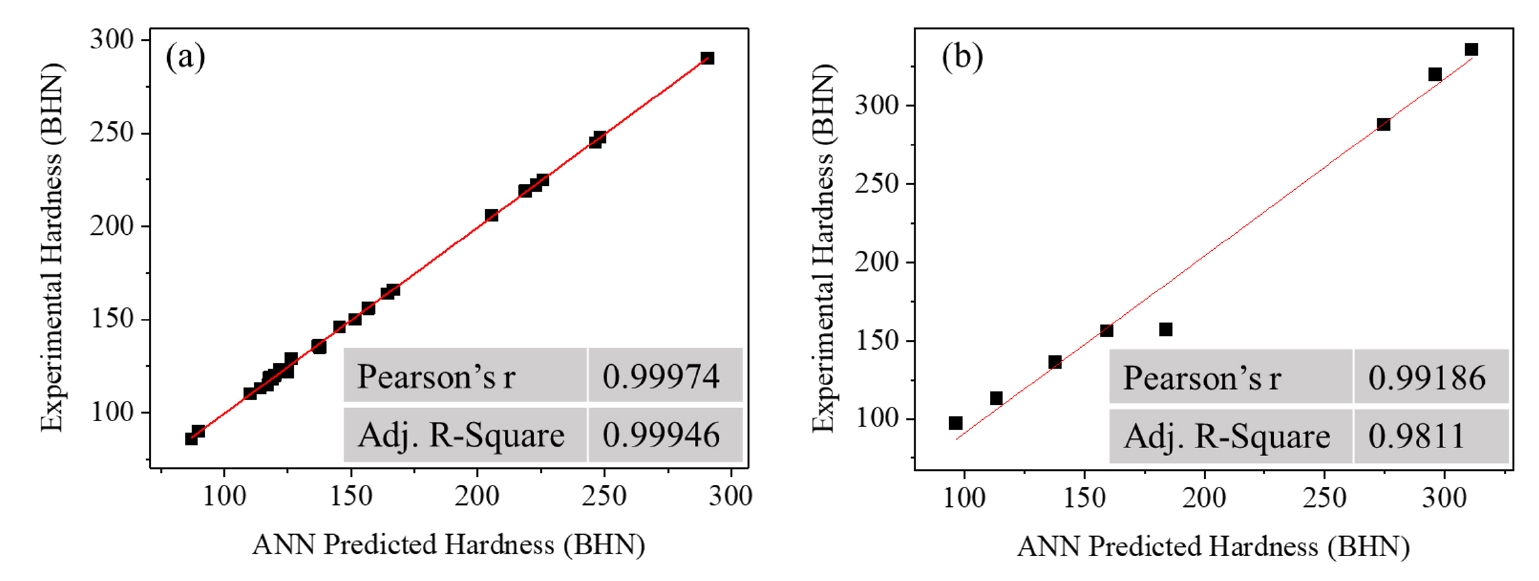
Correlation of experimental and predicted hardness. (a) Training data and (b) unseen testing datasets.
The ANN model relates the input and output through weights and contains information about the relationship between the input and output parameters. Each neuron connected with different weights indicates the strength between input and output data. Model training involves optimizing the weights for better prediction. The weights' magnitude and direction are responsible for the correlation between input and output variables [17]. At the intial iteration, the weights were randomly generated between -0.5 to 0.5. With the increase in the number of iterations, the magnitude of the weights increases considerably in space. These weight values in the elongated space can improve the predictive performance and make the model more reasonable in the case of unknown datasets [21].
3.2. Prediction of the density, hardness, and tensile strength
The developed ANN model can solve the complex relationship by establishing the relationship between input parameters and output prediction. The ANN-predicted output parameters, such as density, hardness, and tensile strength, are shown in Fig. 3, Fig. 4, and Fig. 5, respectively. At the initial milling time, the reinforcement particle B4C distribution was not uniform, and the distance between the particles was also high. As milling time increases, the possibility of breaking big-size B4C particles increases, minimizing the distance between the particles [7]. It can be seen in Fig. 3a that the density of the pressed sample decreases with increasing milling time. This is possible due to prolonged mechanical milling leading to the work hardening in the particles, reducing the deformability during pressing. However, mechanical milling helps in the homogeneous dispersion of B4C particles [23, 24]. It can be seen that with increasing reinforcement volume fraction, the density of composite materials decreases (Fig. 3b). It has been reported that increasing the reinforcement particle size or increasing the volume fraction can increase the yield pressure of the powder materials and reduce the densification rate [25], which is evident in Fig.3a and 3b. This is possible by increasing the reinforcement volume fraction. The work hardening will increase due to increased collision among the particles, so powder becomes more arduous, and pores can't be eliminated during sintering [26].
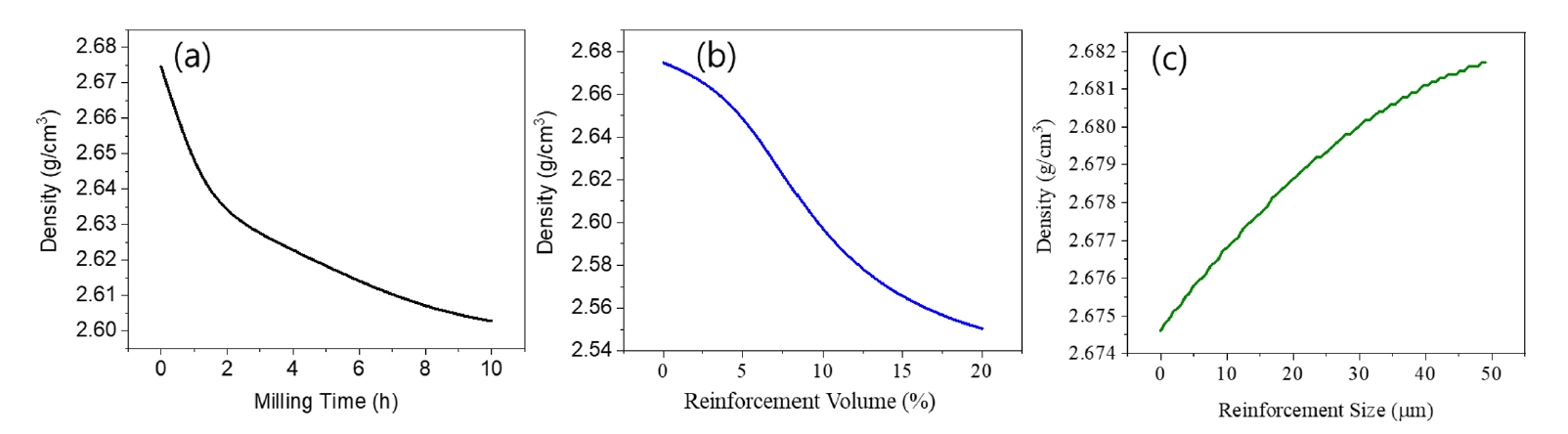
ANN-predicted density according to (a) milling time, (b) reinforcement volume fraction, and (c) reinforcement size.
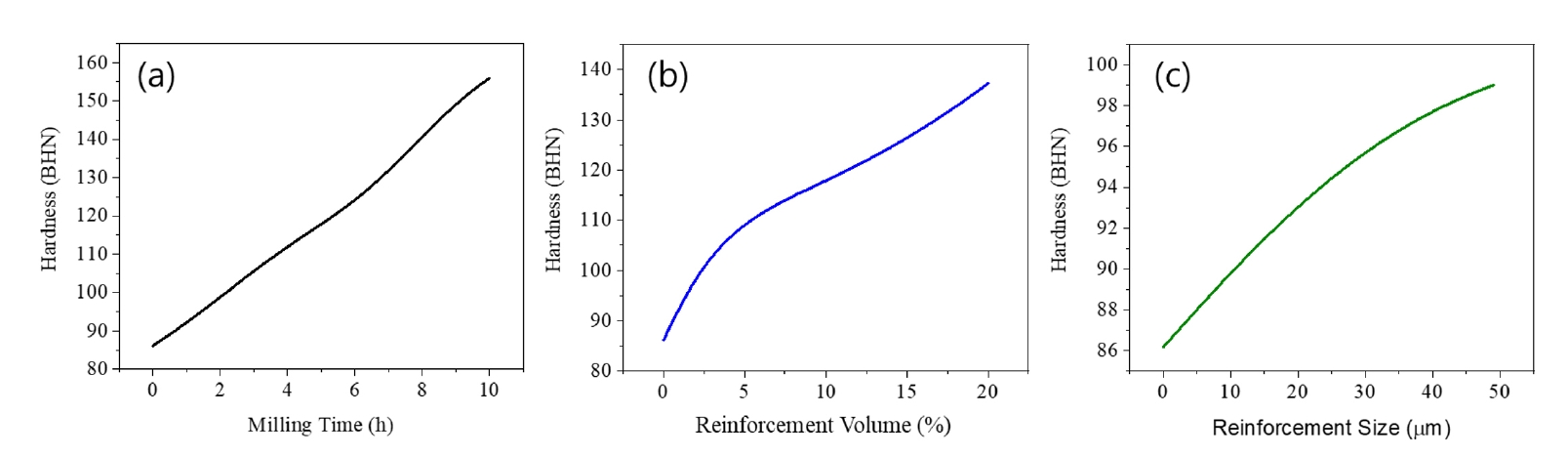
ANN-predicted hardness according to (a) milling time, (b) reinforcement volume fraction, and (c) reinforcement size.
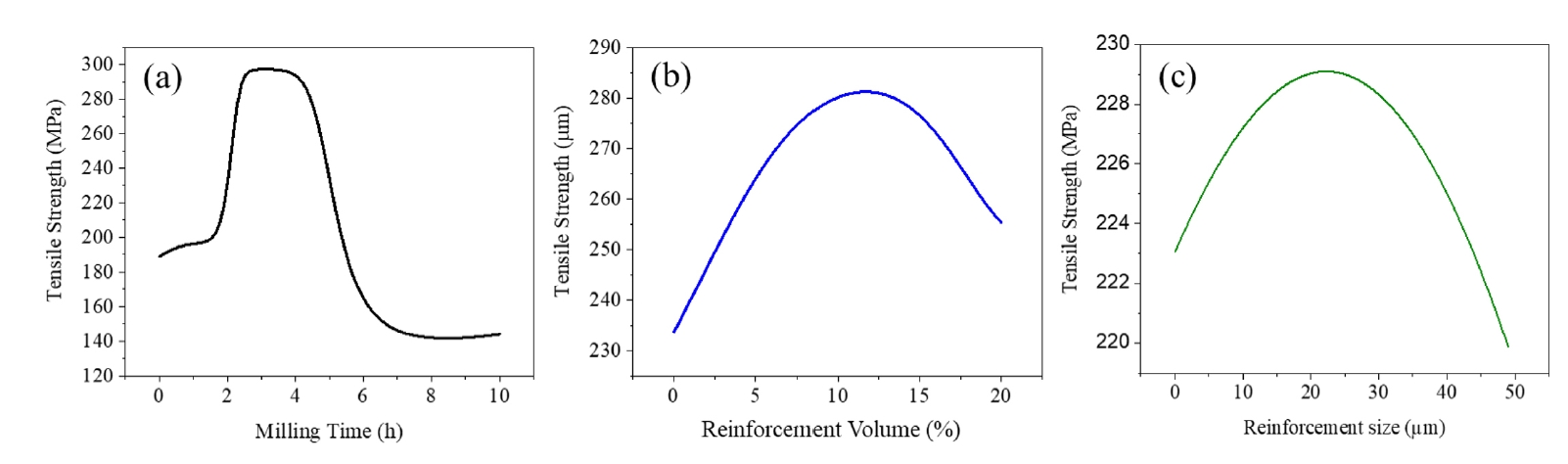
ANN-predicted tensile strength by varying (a) milling time, (b) reinforcement volume, and (c) reinforcement size.
The predicted hardness as a function of input variables is shown in Fig. 4(a-c). It can be seen that the hardness of the sample increases with increasing milling time, reinforcement volume, and reinforcement size. The previous study also observed a similar effect [27] and explained in terms of mechanical milling, which affects the particle distribution and properties in composite material using Al2O3 particle reinforcement. They found two factors affecting hardness: the first factor is the work hardening of matrix material due to mechanical milling, and the second is the role of particles in the matrix. As we know, milling increases the work hardening with milling time, which increases the surface hardness and resists plastic deformation during compaction. This causes an increment in the lattice strain, resulting in higher dislocation density [28]. This phenomenon refines the microstructure and develops a fine microstructure with high stored strain energy. So due to this, the reason the hardness of the sample increases (as depicted in Fig. 4a). With increasing reinforcement volume and reinforcement size, the hardness increases (Fig.4c and d); this may be possible at reinforcement size strain hardening effect would be more and also the hardness inventor tip cover more surface area on the reinforcement particle. Saikeerthi et al. [29] also investigated that the micro-hardness of AMC increased with the B4C particle size and volume fraction of reinforcement. The maximum hardness found was 129 VHN at the particle size of 250μm, and mechanical properties were also improved with the addition of B4C in the aluminum matrix.
The effect of milling time, reinforcement volume fraction, and reinforcement size on the tensile strength of Al-B4C composites are illustrated in Fig. 5. It has been reported that adding brittle, hard ceramic reinforcement makes composite materials brittle and develops interfaces between matrix materials that act as obstacles for dislocation movement during deformation [29]. This results in the interaction of the reinforcing elements with dislocations within the matrix during deformation. The mechanical properties of composite depend on the microstructure and properties of B4C particulates. The high strength is possible if a substantial interface bonding load transfers from the matrix to reinforcement [30]. The strain hardening phenomenon occurs in composites through concentration and interactions of dislocations, hindering the plastic flow due to the presence of reinforcing particles. The distribution of particles in the matrix is also a most important factor affecting the mechanical properties. The distance between the B4C particles increases with an increase in the particle size. The smaller particles distribute homogeneously and show a more significant hindering effect than bigger particles [31]. The uniform distribution of particles reduces the stress concentration points and leads to better load transfer between the matrix and reinforcement, resulting in increased tensile strength. The small particles can provide more grain nucleating agents, which increase the grain refinement effect in the matrix. The smaller grain improves the strength according to the Hall-Petch strengthening mechanism. Whears, in the case of more significant size reinforcement, the stress concentration can increase on the particular reinforcement particle and lead to crack initiation and propagation, reducing the overall tensile strength [32, 33]. This may be the reason for the decrease in the tensile strength after a specific particle size, as shown in Fig. 5c. The strength initially increases with milling time up to 2h milling time and maintains the same strength up to 5h milling time then decreases gradually indicating that the optimal milling time ranging from 2h to 5h (Fig. 5a). This may be possible due to high milling time particle size of the matrix and reinforcement can be more strain hardened and inhomogeneous distribution of B4C particle also possible. This also increases the porosity and reduces the density (Fig. 3a), ultimately reducing the tensile strength [28, 34]. The effect of reinforcement volume on strength is illustrated in Fig. 5b, where an increase in strength is observed with the rising volume fraction of reinforcement up to 11%, then reduced with further increment in reinforcement ratio. This suggests that the aluminum matrix's 11% reinforcement volume is optimum. A higher volume fraction of reinforcement enhances load sharing between the matrix and the reinforcement, reducing stress on the matrix and thus increasing the strength of the composite material. Additionally, a higher volume fraction of reinforcement increases the barriers to dislocation movement within the matrix, further contributing to the material's strength. At a high reinforcement volume, the densification can be reduced due to the agglomeration of particles and porosity [35, 36].
3.3. Index of the relative importance
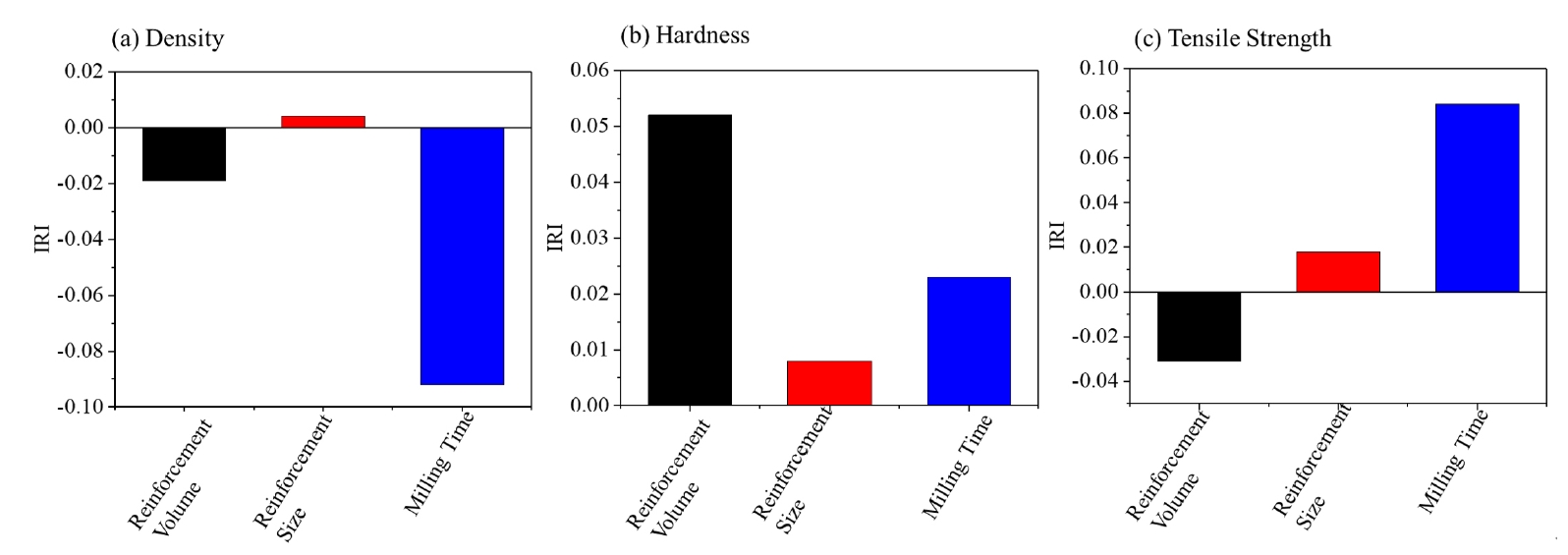
The effect of process parameters on density, hardness, and tensile strength was investigated by the index of relative importance (IRI). IRI is a vector quantity. The magnitude and the direction of IRI indicate the significance of the input process parameters on the output variables. The high values of IRI refer to the high degree of relationship between input and output parameters. A negative value of IRI means that the input parameter has an opponent relationship with output parameters. This study considers the 10% band for each input variable, i.e., +5% and -5%. The IRI plot is shown in the Fig. 6 (a-c). Fig. 6 represents the average IRI of all data sets. We can see that the impact of milling time on density (Fig. 6a) has a robust negative effect among all parameters. This indicates that the milling time is an essential factor affecting the nature of powder materials and the final density. It is found that the distribution of reinforcements and the grain structure of the matrix mainly depend on the milling time. The high milling time applied a high energy impact on particles, which deformed the particles and produced cracks. Deformed and cracked particles can not be densely packed; as a result, the composite may produce porosity [37].
Meanwhile, reinforcement volume is the most robust parameter affecting hardness (Fig. 6b). The positive value indicates that hardness will increase with increasing reinforcement volume. As the volume fraction of reinforcement increases, the total surface area contacting the matrix increases. This larger interface area increases the load transfer efficiency from matrix to reinforcement and acts as a barrier for dislocation movement during plastic deformation; this enhances the hardness [38]. Whereas milling time positively impacts tensile strength (Fig.6b); this may be possible due to sufficiently higher milling time, the homogeneous mixing of reinforcement, particles also getting strained hardened, and more grain refinement occurring [39].
4. Conclusion
The influence of various variables on the density, hardness, and tensile strength of Al2024-B4C was investigated using an ANN model developed from experimental data sets. The model's predictions are highly accurate, with a Mean Absolute Error (MAE) of 3.48 and an adjusted R² value of 0.98. The significance of process variables on output predictions (density, hardness, and tensile strength) was explained using the index of relative importance (IRI). Milling time was identified as the most significant negative influencing parameter on density. Conversely, reinforcement and milling time were the parameters that positively influenced hardness and tensile strength. The effects of other parameters were not significant.
Notes
Conflict of Interest Declaration
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Author Information and Contribution
M.A.K: Researcher, Data Collection and modeling, N.P.L: Senior Researcher, Modeling, and producing the results, W.X.S: Ph.D. Candidate, Interpretation, writing the first draft, N. S. R: Professor, Conceptualization, Editing, and final draft.