Articles
- Page Path
- HOME > J Powder Mater > Volume 29(4); 2022 > Article
-
Article
개선된 회귀착점 방법을 이용한 이방성 적층구조물의 소성해석 - 양승용a, 진두한b,*, 김정한c,*
- Analysis of Anisotropic Plasticity of Additively Manufactured Structure using Modified Return Mapping Method
- Seung-Yong Yanga, Doo-Han Jinb,*, Jeoung-Han Kimc,*
-
Journal of Korean Powder Metallurgy Institute 2022;29(4):303-308.
DOI: https://doi.org/10.4150/KPMI.2022.29.4.303
Published online: July 31, 2022
a 한국기술교육대학교 기계공학부
b 주식회사 타드
c 한밭대학교 신소재공학과
a Korea University of Technology and Education, Chonan, Chungnam, Republic of Korea
b Corporation TAAD, Republic of Korea
c Hanbat National University, Daejeon, Republic of Korea
-
* Corresponding Authors: Doo-Han Jin, TEL: +82-10-7797-4717, E-mail: shrekddu@gmail.com
Jeoung-Han Kim, TEL: +82-42-821-1240, FAX: +82-42-821-1592, E-mail: jh.kim@hanbat.ac.kr - - 양승용.김정한: 교수, 진두한: 책임연구원
• Received: August 11, 2022 • Revised: August 12, 2022 • Accepted: August 22, 2022
© The Korean Powder Metallurgy Institute. All rights reserved.
- 650 Views
- 2 Download
Abstract
- The plastic deformation behavior of additively manufactured anisotropic structures are analyzed using the finite element method (FEM). Hill’s quadratic anisotropic yield function is used, and a modified return-mapping method based on dual potential is presented. The plane stress biaxial loading condition is considered to investigate the number of iterations required for the convergence of the Newton-Raphson method during plastic deformation analysis. In this study, incompressible plastic deformation is considered, and the associated flow rule is assumed. The modified returnmapping method is implemented using the ABAQUS UMAT subroutine and effective in reducing the number of iterations in the Newton-Raphson method. The anisotropic tensile behavior is computed using the 3-dimensional FEM for two tensile specimens manufactured along orthogonal additive directions.
- 유한요소법을 이용하여 재료의 소성변형을 해석할 경우 소성변형의 비선형적 특성으로 인하여 해석적으로 해를 구하기 어려우므로, 수치적으로 반복계산을 이용하여 해를 구하게 된다[1]. 이러한 방법을 회귀착점(return mapping method) 방법이라고 부른다. 일반적으로 뉴튼-랩슨 기법 (Newton-Raphson method, NRM) 이 반복계산 방법으로 널리 사용 된다. 반복계산을 수행하기 위하여는 해의 초기 예측값을 필요로 하고, 이 예측값이 해와 너무 큰 오차가 있을 경우는 반복계산이 해에 수렴하지 못하고 발산하게 된다. 즉 반복 계산을 시작하려면 먼저 미지수인 응력과 등가소성변형률 증분의 초기 추정값이 필요하다. 초기 추 정값이 정해에 근접 하다면 반복계산의 횟수는 단축될 수 있고 수렴성은 증가할 것이다. 기존의 방법은 응력의 값으 로 탄성 예측응력을 사용하고, 등가 소성변형률의 증가는 0으로 가정하는 방식이 널리 사용되고 있다. 그러나 이러 한 방식은 초기 예측응력이 과도하게 크거나, 물질의 이방 성이 심대한 경우, 또는 항복함수가 Tresca 조건과 같이 항복면에 모서리(vertex) 부분을 가진 경우, 반복계산이 해 로 수렴하는데 어려움을 겪게 된다[2]. 본 논문에서는 NRM 반복계산의 수렴성을 증대시키기 위하여 초기 예측 값의 정확도를 향상시킬 수 있는 기법을 이용하였다. 이를 소성예측응력(plastic trial stress) 이라고 칭하기로 한다. 제시된 기법은 소성 변형률 속도 포텐셜 함수(strain rate potential)를 사용하여 응력을 계산하는 방법에 기초하고 있다[3].
- 금속분말을 3D Printing 기법으로 제작한 구조물은 적층 방향에 따라 이방성(anisotropy) 을 나타낸다고 보고되어 있다[4, 5]. 이러한 이방성이 강한 재질에 대하여 Hill의 2 차 이방성 항복 함수를 적용하였고, 소성예측응력(plastic trial stress)을 이용하여 회귀착점 기법을 적용하였다. 3차 원 유한요소법을 적용하여 인장시편의 적층방향에 따른 이방성을 시뮬레이션 할 수 있었다.
- 본 논문의 기술순서는 다음과 같다. 먼저, 2장에서 소성 변형 해석을 위한 일반적인 NRM 반복계산에 대하여 서 술하였으며, 반복계산의 수렴성을 증대시킬 수 있는 소성 예측응력에 대하여 기술하였다. 3장에서는 Hill의 이방성 항복함수에 대하여 설명하였고, 4장에서 단순화된 평면 응력 문제에 대하여 소성예측응력의 수치적 효율성을 검 증하였다. 5장에서는 적층 구조물에 대한 3차원 유한요소 해석을 수행하였으며 시편의 이방성을 성공적으로 나타낼 수 있었다. 본 논문의 소성변형은 연관 유동 법칙(associated flow rule) 을 가정하였고 등방성 소성경화 법칙을 가정하 였다.
1. 서 론
- 소재의 소성변형을 해석하기 위해서는 재료 내부의 응 력 및 소성변형률 값을 시간에 따라 계산하여야 한다. 재 료의 소성거동은 응력과 변형률 사이의 비선형 관계식을 따르고 하중경로에 의존하므로 컴퓨터를 이용해 변형이력 (deformation history)을 따른 수치 해석을 수행하게 된다[1]. 보통 Newton-Raphson 기법(NRM) 을 이용한 반복계산 기 법이 널리 사용되고 있다. NRM 반복계산법은 구하고자 하는 물리량에 대한 초기 예측을 한 후 변수 사이의 부정 합에서 기인하는 잔류오차(residual)의 크기를 줄이기 위한 보정 과정을 거치게 된다. 여기서 초기 예측값의 정확도에 따라 반복계산의 횟수는 변하게 된다[2]. 따라서 초기 예 측값을 얼마나 정확하게 예측하느냐가 계산 시간 및 반복 계산 횟수를 결정하는 중요한 요소이다.
- 먼저, 회귀착점 방법에서의 NRM 반복계산의 개요는 다 음과 같다. 현재의 응력을 σij(t) 라 하고 변형률 증가량 Δεij 가 재료에 가해져서 다음 시간에서의 응력 σij(t + Δt) 을 구하고자 한다. 변형률 증가량 동안 소성변형이 발생한다 면 먼저 항복조건이 만족되어야 한다. 항복함수를 ϕ(σij) 라 고 표시하고, 등방성 소성경화함수를 등가소성변형률 의 함수
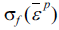 로서 나타낸다면, 항복조건은 다음 식 과 같다.
로서 나타낸다면, 항복조건은 다음 식 과 같다. - 여기서 방정식은 시간 t + Δt 에서 성립하고, 내연적 오일 러 방정식(implicit Euler method)을 적용하기로 한다. 연관 유동 법칙(associated flow rule)을 적용하면 소성변형률 증 분은 다음 식을 만족하여야 한다[6].
- 여기서 소성변형률 증가량
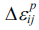 은 전체 변형률 증가량 Δεij 에서 탄성 변형률 증가량
은 전체 변형률 증가량 Δεij 에서 탄성 변형률 증가량 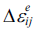 을 제외한 값이 된다. 즉, 여기서 C는 탄성계수를 나타내는 텐서이다. (3)식을 (2)식 에 대입하면 다음과 같은 잔류오차 R을 정의할 수 있다.
을 제외한 값이 된다. 즉, 여기서 C는 탄성계수를 나타내는 텐서이다. (3)식을 (2)식 에 대입하면 다음과 같은 잔류오차 R을 정의할 수 있다. - 또한 (1)식의 성립 유무를 판단하여야 하므로 잔류 오차 를 다음과 같이 정의할 수 있다.
- NRM 반복계산(iteration)은 위의 두 가지 잔류오차가 정 해진 허용한도보다 작을 때까지 계속된다. 다음과 같은 전 체 목적함수(merit function)를 정의하면 편리하다[2].
- 매 반복계산에서 목적함수가 감소하는 방향으로 변분량 δσ 과
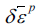 을 결정하고 그 값을 누적한다. 계산과정에서 항복함수의 1계 및 2계 도함수가 필요하다[2].
을 결정하고 그 값을 누적한다. 계산과정에서 항복함수의 1계 및 2계 도함수가 필요하다[2]. - 본 논문에서는 초기응력으로 탄성응력 대신 다음과 같 이 소성변형률 속도 포텐셜 함수(plastic strain rate potential)에 의해 정의되는 소성응력을 사용하고자 한다 [3]. Hill은 연관유동법칙에서 항복함수 ϕ(σ)에 대응하는 소성변형률 속도 포텐셜을 정의하였다[7]. 이 함수를 ψ (Δε p)라고 표시한다. 이 때, 연관유동법칙 (2)에 대응하 는 응력 법칙이 다음과 같이 존재함을 제시하였다.
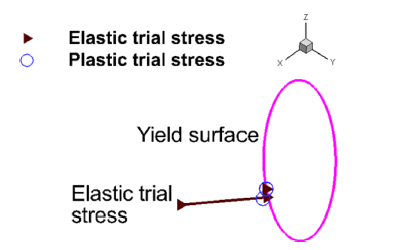
- 위 식에서 정의되는 응력은 소성변형하는 물체의 응력 상태를 나타낸다. 본 논문에서는 이 응력을 초기 예측응력 으로 이용하고자 한다. 구체적으로 Fig. 1에 기존의 탄성 예측응력 σ tr을 표시하였고, 반경회귀 방법[8]을 사용하여 현재 시간 t(또는 스텝 n) 에서의 항복면과 만나는 응력을 αyσ tr이라고 할 때(단 0 ≤ α ≤ 1), 반경 소성변형률 증분(radial plastic strain increment)을 다음 식으로 정의할 수 있다.
- 이에 해당하는 등가 소성변형률 증분은 변형률 포텐셜 을 이용하여 이 되며, 위와 같이 등가 소성변형률 증분이 주어졌다면 소성 포텐셜 함수의 도함수를 이용하여 NRM의 초기 예 측응력을 (7)식으로 정의할 수 있다. 위의
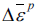 와 σ를 초 기 예측값으로 이용하였다.
와 σ를 초 기 예측값으로 이용하였다. - Fig. 2에 회귀착점 계산 과정에서의 응력의 변화를 나타 내었다. 초기 탄성예측 응력이 3축 주응력이고 그 값이 (σxx, σyy, σzz) = (1825.9, -1192.4, -635.9) MPa 인 경우 응력 의 수렴 경로가 삼각형 실선으로 표시되었고, 소성예측응 력일 경우 초기 예측응력은 (σxx, σyy, σzz) = (753.8, -190.7, -565.5)이고 수렴경로가 동그라미 점으로 표시되었다. 그 림에서 볼 수 있듯이, 소성예측응력의 경우가 항복면에서 가까운 위치에서 반복계산을 시작한다는 것을 볼 수 있다. 그림에서 예로 든 항복면은 3장에서 기술할 적층제조된 스테인레스 강의 항복면을 이용하였다.
2. 회귀착점 방법과 뉴튼-랩슨 반복계산법(NRM)
- 본 논문에서는 적층제조 기법으로 제작된 재료의 이방 성을 나타내기 위한 항복함수로 Hill의 2차 항복함수를 사 용하였다. 항복함수의 식은 다음과 같다[6].
- σij는 실험실 좌표계방향의 응력성분을 나타낸다. F, G, H, L, M, N은 물질의 비등방성을 표현하는 계수이다. 만약 F = G = H = 1, L = M = N = 3이라면 v on Mises 등방성 항 복함수에 해당한다. Hill의 이론에 따르면, 각 항복함수에 는 쌍대관계(duality relation)에 있는 소성변형률 속도 포텐 셜 함수가 정의된다. (10)식에 해당하는 쌍대포텐셜 함수는 으로 가정할 수 있다. 여기서 계수 Bi는 다음의 Hill의 쌍 대관계식을 만족시키도록 결정된다.
- 위 두 식의 의미는 항복면 상에서 계산된 유동벡터가 일 정한 값의 소성변형률 포텐셜 값을 가지고, 소성변형률 포 텐셜 상에서 계산된 법선벡터가 일정한 항복함수 값을 가 짐을 나타낸다. 2차 항복함수일 경우 해석적으로 쌍대 포 텐셜 함수가 구해질 수 있다[3].
- Shen 등[5]은 스테인레스 강의 적층제조 방향에 대한 인 장강도를 측정하였다. 측정결과에 의하면 항복강도는 A, B, C 세 방향에 대하여 0.48:0.5:1의 비율로 측정되었다. (A,B,C의 방향은 참고문헌[5] 참조.) 실험결과를 이용하여 3D Printing 된 스테인레스 강의 이방성 계수를 다음과 같 이 가정하였다.
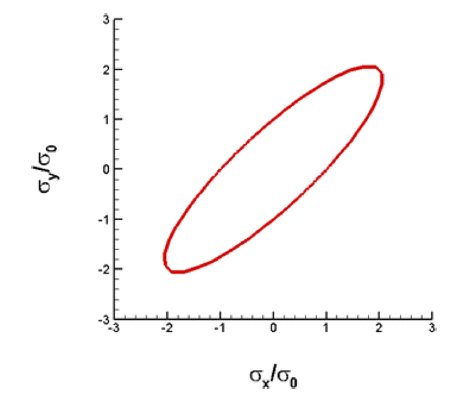
- 여기서 X는 A 방향으로의 1축 인장시의 항복응력 값이다 (즉 X = σf). 전단응력에 대한 이방성은 실험에서 측정되지 않았으므로 등방성 계수로 가정하였다. 따라서 항복조건 식은 이다. 위의 항복함수는 볼록함수(convex function) 조건을 만족시킴을 확인할 수 있다. 이에 해당하는 소성변형률 속 도 포텐셜 함수는 이다. Figs. 3과 4에 고려한 이방성 스테인레스 강[5]의 항 복면과 포텐셜면을 도시하였다.
3. Hill의 이방성 2차 항복함수와 소성변형률 속도 포텐셜
Fig 4
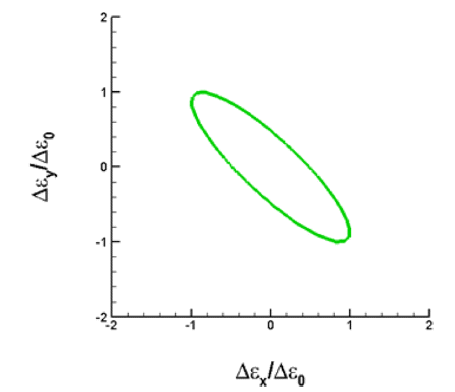
Plastic strain rate potential surface corresponding to the yield surface in Fig. 3 with ψ (Δε p/Δε p0) = 1.

- 이번 절에서는 기존의 탄성예측응력과 본 논문에서 제 시한 소성예측응력 사이의 정량적인 비교를 통하여, 회귀 착점 계산에서의 소성예측응력의 수치적 효율성을 확인하 고자 한다. 탄소성 문제의 조건은 2축 주응력이 가해지는 평면 응력 문제를 고려하였다(따라서 σzz = 0). 사용한 스 테인레스 강[5]의 탄성계수는 160 GPa, 푸아송비는 0.3, 초 기항복강도는 500 MPa, 선형 소성경화계수는 40 GPa로 가 정하였고, 항복함수의 비등방성 계수는 3절에 기술하였다.
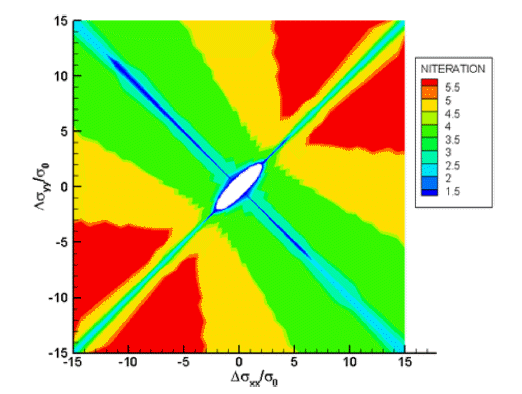
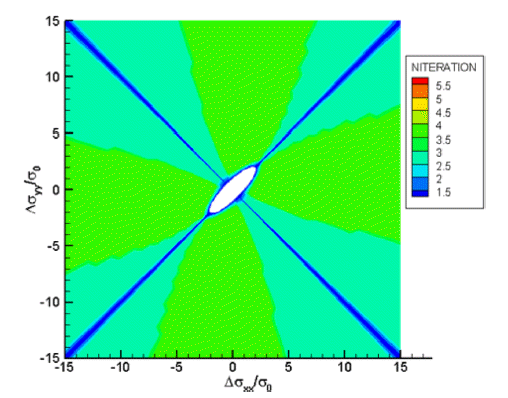
- Figs. 5과 6는 초기에 응력이 없는 상태에서 2축 주응력 Δσxx 와 Δσyy 이 가해졌을 때 회귀착점 방법에 의해 NRM 축차가 새로운 해로 수렴하기 위한 반복계산횟수를 나타 낸 그림이다. 소성예측응력(plastic trial stress)이 탄성예측 응력에 비하여 적은 수의 반복계산이 필요함을 볼 수 있 다. 이의 원인은 소성예측응력이 항복면에 가까운 응력상 태에서 반복계산을 시작하기 때문인 것으로 판단된다.
4. 수치계산을 통한 수렴속도 검증
- 본 절에서는 3D Printing된 스테인레스 강[5]을 이방성 소재로 모델링 하여 유한요소법으로 인장시험을 시뮬레이 션 한 결과를 제시하였다. 인장시편의 방향은 Fig. 7에 표 시된 바와 같이 적층방향 z’과 그에 수직한 방향 x’의 2가 지를 고려하였다. 3절에서 기술한 바와 같이 스테인레스 강의 이방성을 정의하기 위하여, 참고문헌[5]를 이용하였 으며, 적층방향 z’ 방향으로 2배의 항복강도를 가진다고 가정하였다. 이러한 소재의 이방성을 Hill의 항복함수로 모델링하였으며, 이를 ABAQUS/Standard[9]의 UMAT 서 브루틴으로 작성하였다. 시편의 인장방향을 z’ 로 설정하 기 위하여 ABAQUS의 *orientation 명령어를 이용하여, 다음과 같이 재료의 로컬 좌표축을 실험실 좌표축에 상대 적으로 경사지도록 설정하였다.
- *orientation,
- 0., 1., 0., 0., 0., 1.
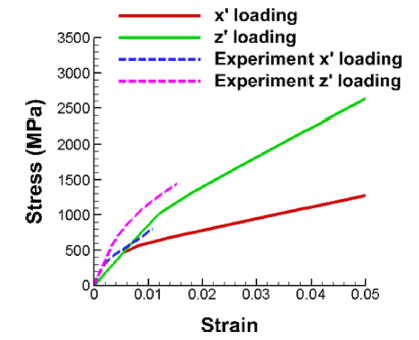
- Fig. 8은 두 가지 인장시편에 대한 공칭응력과 공칭변형 률 곡선을 유한요소해석 결과로부터 도출한 것이다. 초기 항복응력 값은 x’ 방향으로 대략 500MPa 이고 z’ 방향으 로 1000MPa 인 것을 확인할 수 있다. 또한 변형경화 하 는 동안 z’ 방향으로 대략 2배의 항복강도를 나타내는 것 을 확인할 수 있다. 이는 참고문헌[5]의 실험에서 관찰한 바와 동일하다. 구체적으로 실험결과와 시뮬레이션 결과 를 비교해 보면 탄성영역을 제외하며 거의 동일함을 확인 할 수 있다. 계산에 사용된 탄성계수의 값과 이방성 항복 함수의 계수를 정밀하게 조정한다면, 계산결과가 실험결 과와 더욱 일치하도록 조정할 수 있으리라 판단된다.
5. 이방성 적층 제조된 인장시편의 모델링
Fig. 7
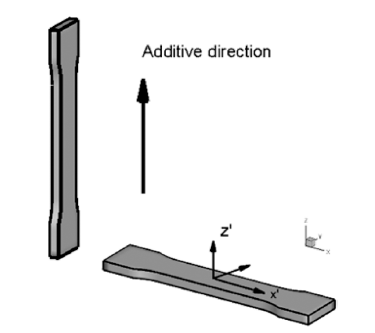
Specimen directions of additively manufactured stainless steel. Z’ is the additive manufacturing direction.

- 본 논문에서는 회귀착점(return mapping) 방법의 수렴속 도를 향상시키고자 Hill의 쌍대 포텐셜 이론에 기반한 소 성예측응력(plastic trial stress)을 뉴튼-랩슨 방법의 초기예 측응력으로 사용하였다. 소성예측응력의 수치적 효율성을 검증하기 위하여, 2차원 평면 주응력 조건을 이용하였으 며, 모든 응력의 조합에서 반복계산 횟수가 줄어드는 결과 를 확인할 수 있었다. 3D Printing에 의해 적층제조된 구 조물은 강한 이방성을 나태 내므로, 이를 모델링 하기 위 하여 2차 이방성 항복함수와 이에 대응하여 소성변형률 속도 포텐셜 함수를 사용하였다. 적층 방향과 이에 수직인 방향으로의 인장 시편을 고려하였으며, ABAQUS UMAT 유한요소 해석을 통하여 실험에서 관찰된 수직방향으로의 이방성을 성공적으로 시뮬레이션 할 수 있었다.
6. 결 론
-
Acknowledgements
- 이 논문은 2021년도 한국기술교육대학교 교수 교육연구 진흥과제 지원에 의하여 연구되었음.
감사의 글
- 1. E. A. de Souza Neto, D. Peric and D. R. J. Owen: Computational Methods for Plasticity: Theory and Applications, Wiley (2008)..
- 2. W. M. Scherzinger: Comput. Methods Appl. Mech. Eng., 317 (2017) 526..Article
- 3. S.-Y. Yang and W. Tong: NUMISHEET 2022, Proceedings of the 12th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes, (2022) 3..
- 4. R. Wauthlea, B. Vrancken, B. Beynaerts, K. Jorissen, J. Schrooten, J.-P. Kruth and J. V. Humbeeck: Addit. Manuf., 5 (2015) 77..Article
- 5. L.-C. Shen, X.-H. Yang, J.-R. Ho, P.-C. Tung and C.-K. Lin: Materials, 13 (2020) 5142..ArticlePubMedPMC
- 6. R. Hill: The Mathematical Theory Of Plasticity, Oxford Univ. Press, (1998).
- 7. R. Hill: J. Mech. Phys. Solids, 35 (1987) 23..Article
- 8. R. D. Krieg and D. B.Krieg: Accuracies of Numerical Solution Methods for the Elastic-Perfectly Plastic Model, J. Pressure Vessel Technol., 99 (1977) 510..Article
- 9. ABAQUS 6.13 Documentation. Dassault Systemes..
Figure & Data
References
Citations
Citations to this article as recorded by 

Analysis of Anisotropic Plasticity of Additively Manufactured Structure using Modified Return Mapping Method
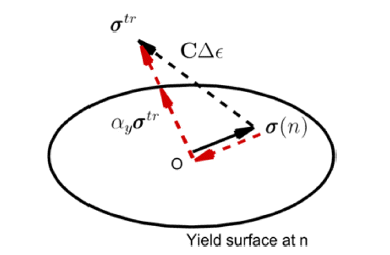
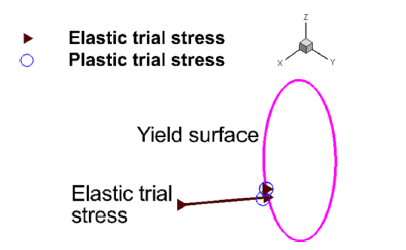
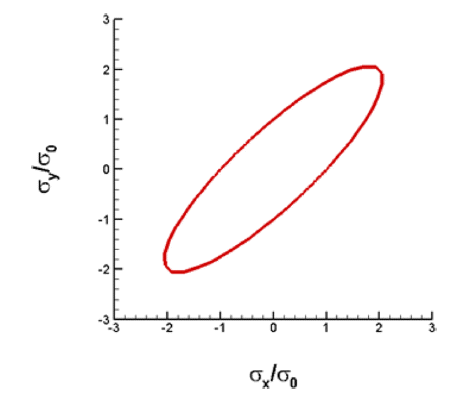
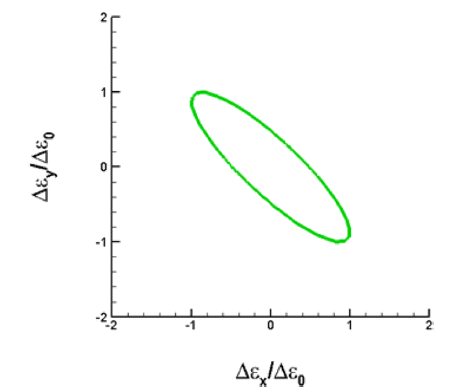
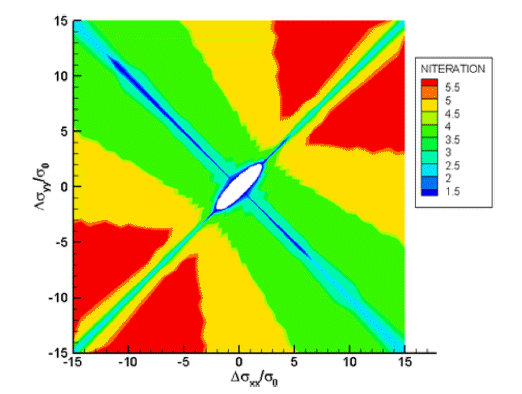
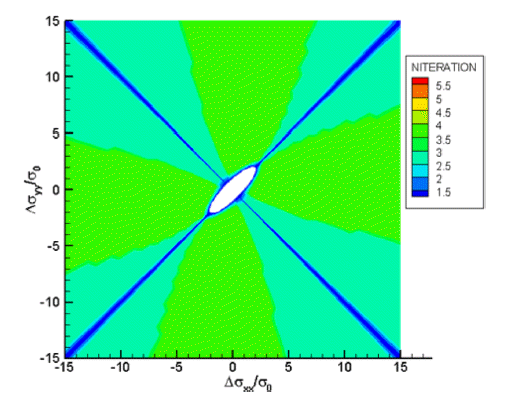
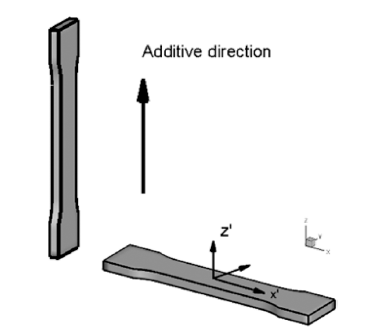
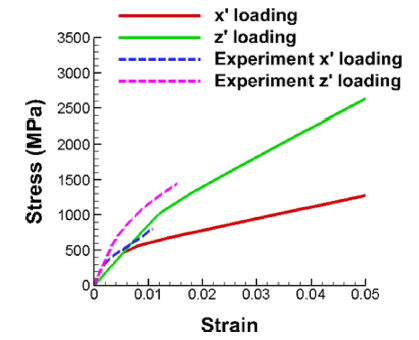
Fig. 1
Schematic picture of radial return mapping algorithm.
Fig. 2
Return mapping stress trajectories of elastic and plastic trial stresses for the considered stainless steel.
Fig 3
Plane stress yield surface of anisotropic stainless steel with ϕ (σ /σ0) = 1.
Fig 4
Plastic strain rate potential surface corresponding to the yield surface in Fig. 3 with ψ (Δε p/Δε p0) = 1.
Fig 5
Number of iterations for elastic trial stress. σ0 is the normalizing initial yield strength.
Fig 6
Number of iterations for plastic trial stress. σ0 is the normalizing initial yield strength.
Fig. 7
Specimen directions of additively manufactured stainless steel. Z’ is the additive manufacturing direction.
Fig. 8
Nominal stress vs nominal strain curves of x’ and z’ tensile loading directions.
Fig. 1
Fig. 2
Fig 3
Fig 4
Fig 5
Fig 6
Fig. 7
Fig. 8
Analysis of Anisotropic Plasticity of Additively Manufactured Structure using Modified Return Mapping Method
TOP
 KPMI
KPMI

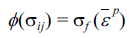
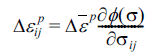
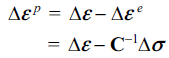
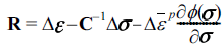
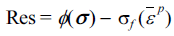
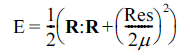
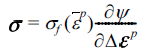

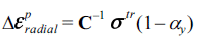
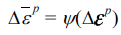
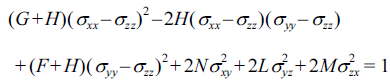
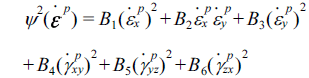
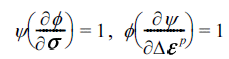
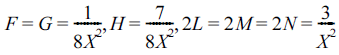
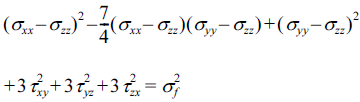
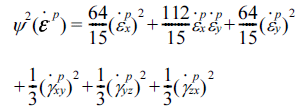
 ePub Link
ePub Link Cite this Article
Cite this Article