Articles
- Page Path
- HOME > J Korean Powder Metall Inst > Volume 22(4); 2015 > Article
-
Article
- Atomistic Simulation of Sintering Mechanism for Copper Nano-Powders
- Yujin Seong, Sungwon Hwang, See Jo Kima, Sungho Kimb, Seong-Gon Kimc, Hak Jun Kimd, Seong Jin Park*
-
Journal of Korean Powder Metallurgy Institute 2015;22(4):247-253.
DOI: https://doi.org/10.4150/KPMI.2015.22.4.247
Published online: July 31, 2015
Department of Mechanical Engineering, POSTECH, 77 Cheongam-Ro, Nam-Gu, Pohang, Gyeongbuk 790-784, Korea
a Department of Mechanical Design Engineering, Andong National University, 1375 Gyeongdon-Ro, Andong, Gyeongbuk 760-749, Korea
b Center for Computational Sciences, Mississippi State University, P.O.Box 5405, Starkville, MS 39762, USA
c Department of Physics and Astronomy, Mississippi State University, P.O.Box 5405, Starkville, MS 39762, USA
d Agency for Defense Development, 111 Sunamdong, Yuseonggu, Daejeon 305-152, Korea
- * Corresponding Author: Seong Jin Park, TEL: +82-54-279-2182, FAX: +82-54-279-5899, E-mail: sjpark87@postech.ac.kr
© The Korean Powder Metallurgy Institute. All rights reserved.
- 1,297 Views
- 11 Download
- 3 Crossref
Abstract
- The sintering mechanisms of nanoscale copper powders have been investigated. A molecular dynamics (MD) simulation with the embedded-atom method (EAM) was employed for these simulations. The dimensional changes for initial-stage sintering such as characteristic lengths, neck growth, and neck angle were calculated to understand the densification behavior of copper nano-powders. Factors affecting sintering such as the temperature, powder size, and crystalline misalignment between adjacent powders have also been studied. These results could provide information of setting the processing cycles and material designs applicable to nano-powders. In addition, it is expected that MD simulation will be a foundation for the multi-scale modeling in sintering process.
- Nanostructured materials have been paid attentions increasingly because those materials exhibit exciting properties than that of bulk materials and hold great promise for various technological applications. Sintering is the simplest and most cost effective processing technique to produce density-controlled materials and components from metal or/and ceramic powders by applying thermal energy. The main challenge of sintering nano-particles is to avoid coarsening during consolidation to keep the nanostructure of final component. The Hall-Petch effect, which is mechanical strength increases with smaller grain sizes at nanoscale under 100 nm, is evidence of the importance to nano-grained materials. Therefore, it is important to understand the sintering behavior of nano-powders.
- Molecular dynamics (MD) simulations is a tool to investigate the sintering of nano-powders [1-8]. MD simulations of sintering for face-centered cubic metals such as copper [1, 3, 7-8], gold [3, 7], palladium [4-5], aluminum [2], silver [7] and body-centered cubic metals such as tungsten [6] have been carried out to investigate factors affecting densification behaviors such as the size and shape of powders, and temperatures. These simulations require accurate atomic interaction potential to compute the energy of each atom in the system. First-principles calculations give us the most reliable inter-atomic potentials. However, sintering simulations of nano-powders is essential to have a large number of atoms that render these methods impractical because of cost efficiency of computer. An alternative is to use empirical or semi-empirical inter-atomic potentials. Here, we use the embeddedatom method (EAM)[9-10], which is in good agreement with experiments or first principles calculations.
- In this paper, the sintering mechanism of nanoscale copper powders has been investigated for initial-stage sintering using a molecular dynamics (MD) simulation with the embedded-atom method (EAM). The mechanism of the initial-stage sintering has been studied using the activation energy of five sintering mechanisms with the two-particle model and then the effects of temperature, powder size, and misorientation between two powders were discussed further.
1. Introduction
- Molecular dynamics (MD) simulation carried out using the LAMMPS [11], which is one of open sources of MD simulation. The embedded-atom method (EAM) approach was employed to describe the motion of atoms. Within the EAM approach [9-10], total energy E of a system of atoms is written as the sum of the atomic energies,
- with the atomic energy being the sum of two contributions,
- where V(rij) is an interatomic pairwise potential, and F(ρi) is the embedding energy function of the local “atomic density” at the site of atom i. The interatomic pairwise potential represents the interaction between an individual atom and its neighbor as a function of the relative distance rij. The embedding energy describes the interaction among the electronic orbitals of the atoms in the solid. A non-dimensional term ρi is also considered as the contribution of each neighbor atom to the electronic density of the particular atom,
- In this paper, EAM parameters of Cu proposed by Mishin et al. [12] are used for the simulations.
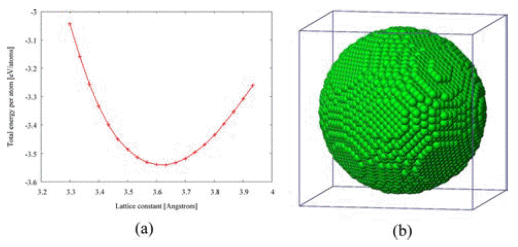
- The two-powder sintering problem was set as shown in Fig. 1. The powders consist of a spherical fcc Cu structure with radius ranging from 2.896 to 5.439 nm (17,118- 113,040 atoms). There is no external pressure surrounding the powders, i.e., the surface of powders is set to free. To determine optimum lattice constant of fcc Cu crystal, the total energy per atom as a function of the lattice constant is calculated, as shown in Fig. 2(a). Fig. 2(b) shows a nano-powder with radius 3.982 nm built using the optimum lattice constant 0.362 nm. The number of the atoms is 22,279 and sufficient to simulate thermal behavior. Initial configuration is prepared by randomizing the velocities of atoms in the nano-powders according to the Maxwell-Boltzmann distribution at the room temperature.
2. Modeling and Simulations
- 3.1. Non-isothermal sintering
- We began with a non-isothermal sintering problem where the temperature is set with a thermal cycle from 300 K to 1,500 K with increment of 300 K at every 25 ps interval. Fig. 3 shows the evolution of two-powders sintering. As the temperature increases, the neck between two powders grows initially and then these powders merge into one powder above 1,200 K.
- 3.2. Isothermal sintering and temperature effect
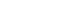
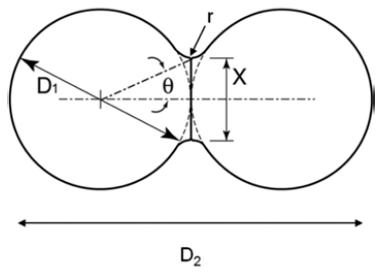
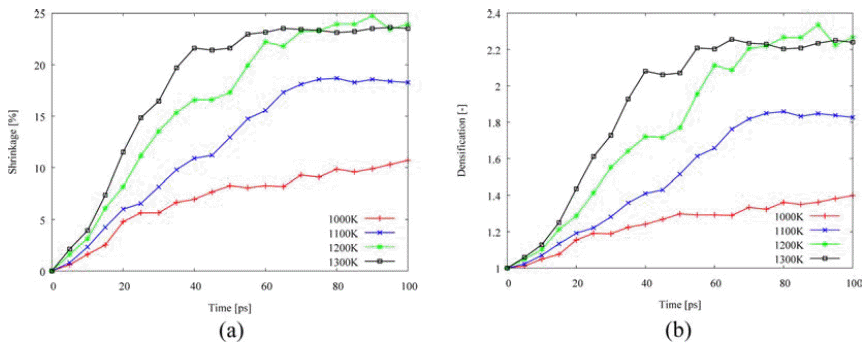
- Next, isothermal sintering problems carried out to study dimensional changes in detail. The temperature was chosen to 1,000K, 1,100K, 1,200K, and 1,300K and the sintering time was set to 100 ps. As shown in Fig. 1, the dimensional changes such as the characteristic length D1, and D2, the neck growth X, and the neck angle θ were measured. Fig. 4(a) shows the evolution of isothermal sintering as a function of the dimensional changes. The diameter of each powder D1 increases, while the longest length of two powders D2 reduces over time during the sintering. Fig. 4(b) shows the neck growth X, which is calculated from the geometric relation between D1 and D2. The neck forms very abruptly at 15 ps and grows quickly for the next 10 ps and then the neck growth is saturated. The geometric information changes even below melting point, implying the pre-melting surface because atomic velocities are increased at higher temperature.
- The apparent activation energy for initial-stage sintering is calculated using two-particle model and linear regression calculation as shown in Fig. 5 and Table 1. The two-particle model is reported in a previous study [6]. The lowest activation energy is for viscous or plastic flow among the five sintering mechanisms, which may reflect the dominance of the pre-melting layer. At initial stage of sintering, atoms are diffusive near the contact region between two nano-powders. The calculated activation energies in this study are lower than reference value [13]. Especially, the grain boundary diffusion has the largest difference with reference value in the activation energy among the mechanisms. The difference reflects the lack of a grain boundary due to the perfect alignment of crystalline structures between them.
- Fig. 6 shows the densification behaviors for the isothermal sintering as functions of shrinkage and densification, ρ/ρo, which were calculated by two-particle model. As temperature is increased, the shrinkage and the densification increase. Therefore, the higher temperature enhanced shrinkage and densification in two-particle model.
- 3.3. Particle size effect
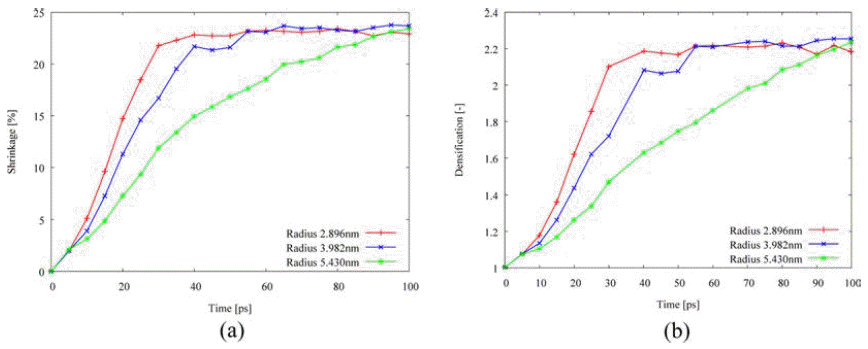
- Fig. 7 shows the effect of powder size on the densification behavior. At the smaller powder size, the shrinkage and the densification early increases and quickly reach the saturated value. The activation energy with various particle sizes is listed in Table 2. The energy associated with viscous or plastic flow and evaporation-condensation slightly increase as the powder size is increased, while other three mechanisms such as lattice, grain-boundary, and surface diffusion highly increase with the higher powder size. It is implied that the smaller powder size enhance the densification behavior due to the ratio between the surface and the volume, i.e., the smaller powder size is helpful to the active atomic transport to the center from the surface.
- 3.4. Misorientation effect
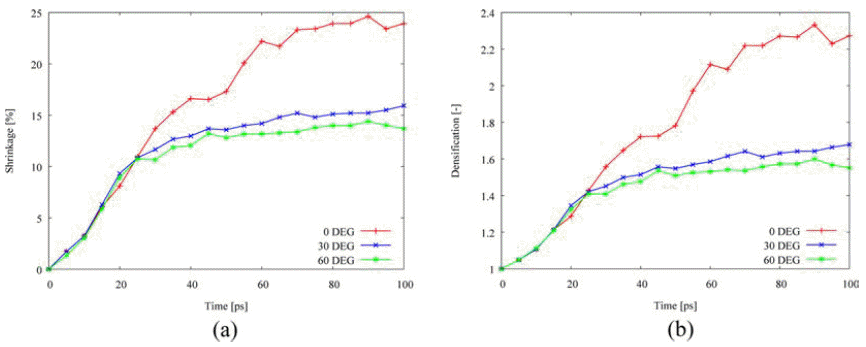
- Fig. 8 depicts the misorientation effect on the densification behavior. The tilt angles with <100> misorienation axis are selected to 0°, 30°, and 60°. Misorientation reduces the shrinkage and the densification so that the densification behavior is affected by the tilt angle due to the tilt grain boundary. It is consistent with previous studies on the effect of tilt grain boundary on diffusion that the grain boundary energy in a range of tilt angle between 0° and 90° has a parabolic shape and maximum value occurs around 45° for face-centered cubic metals [4, 14-15]. As listed in Table 3, the activation energy on grain boundary diffusion remarkably increases among the other mechanisms, following the increased energy on lattice and surface diffusion.
3. Results and Discussions
Evolution of sintering of copper nano-powders: (a) 300K, 0ps, (b) 600K, 25ps, (c) 900K, 50ps, (d) 1,200K, 75ps, and (e) 1,500K, 100ps.

Evolution of isothermal sintering at different temperatures: (a) dimensional changes, (b) change of neck growth, and (c) change of neck angle.
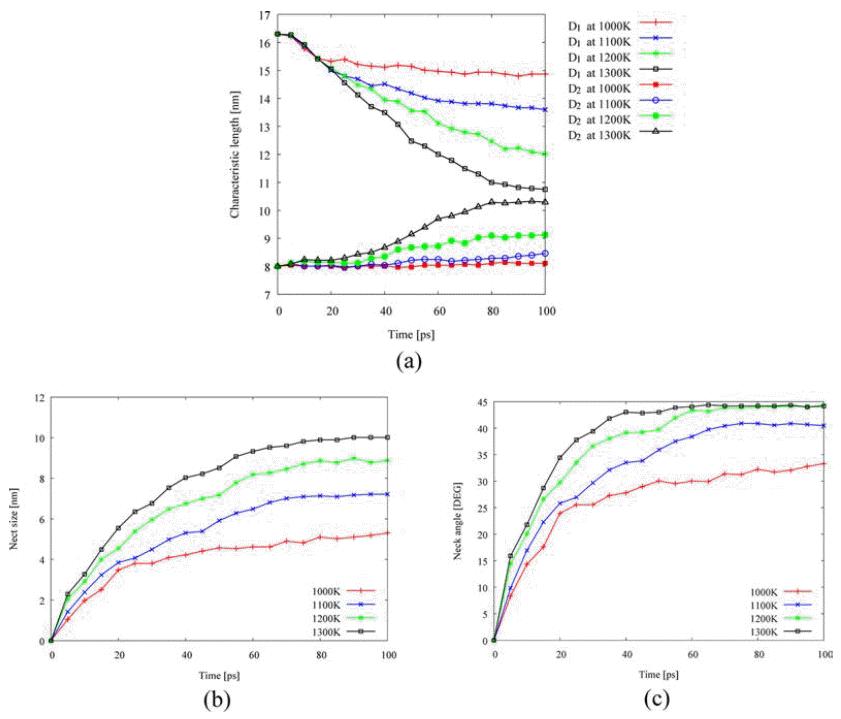
Linear regression to obtain apparent activation energy on five sintering mechanisms: (a) viscous or plastic flow, (b) evaporationcondensation, (c) lattice (volume) diffusion, (d) grain-boundary diffusion, and (e) surface diffusion.
Activation energy for five sintering mechanisms
| Sintering mechanism | Activation energy (kJ/mol) | |
|---|---|---|
|
|
||
| Two-particle model | Ref. [13] | |
|
|
||
| Viscous flow or Plastic flow | 63.97 | 197 |
| Evaporation-condensation | 86.91 | 307 |
| Lattice(volume) diffusion | 145.18 | 213 |
| Grain-boundary diffusion | 168.85 | 107 |
| Surface diffusion | 203.70 | 205 |
Activation energy with various particle sizes
Effect of misorientation on the densification behavior: (a) shrinkage, and (b) densification.
Activation energy with various tilt angles between two powders
- Sintering mechanisms of two copper nano-powders at initial-stage sintering have been investigated using the MD simulation. The densification behavior during the sintering was measured using the geometric information such as the neck growth and the neck angle and then the activation energy associated with atomic transport was calculated using the two-particle model. The MD simulation results implied presence of pre-melting layer on surface of copper so that this layer gives low activation energy for viscous or plastic flow. Moreover, the activation energy for grain-boundary diffusion is relatively higher than experimental values due to the perfect orientation between two powders.
- There are two factors affecting on the densification behavior such as the powder size and the misorientation between two powders. The smaller powder size makes the densification earlier due to the surface-volume ratio so that the smaller size gives low activation energy, especially on lattice, grain-boundary, and surface diffusion. The tilt grain boundary due to the misorientation makes the activation energy higher, which is consistent with previous studies on the effect of tilt grain boundary on diffusion.
4. Conclusions
-
Acknowledgements
- This work was supported in part by the Defense Research Laboratory Program of the Defense Acquisition Program Administration and the Agency for Defense Development of Republic of Korea under the contract UD110089GD and the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2011-0030075).
Acknowledgements
- 1. H. Zhu and R. S. Averback: Mater. Sci. Eng., 204 (1995) 96. .Article
- 2. J. S. Raut, R. B. Bhagat and K. A. Fichthorn: Nanostruct. Mater., 10 (1998) 837. .Article
- 3. P. Zeng, S. Zajac, P. C. Clapp and J. A. Rifkin: Mater. Sci. Eng., 252 (1998) 301. .Article
- 4. A. J. Haslam, S. R. Phillpot, D. Wolf, D. Moldovan and H. Gleiter: Mater. Sci. Eng., 318 (2001) 293. .Article
- 5. V. Yamakov, D. Moldovan, K. Rastogi and D. Wolf: Acta Mater., 54 (2006) 4053. .Article
- 6. A. Moitra, S. Kim, S.-G. Kim, S. J. Park, R. M. German and M. F. Horstemeyer: Acta Mater., 58 (2010) 3939. .Article
- 7. F. Hussain, S. S. Hayat, M. Imran, S. A. Ahmad and F. Bouafia: Comput. Mater. Sci., 65 (2012) 264. .Article
- 8. B. Cheng and A. H. Ngan: Int. J. Plast, 47 (2013) 65. .Article
- 9. M. S. Daw and M. I. Baskes: Phys. Rev. B, 29 (1984) 6443. .Article
- 10. M. S. Daw, S. M. Foiles and M. I. Baskes: Mater. Sci. Rep., 9 (1993) 251. .Article
- 11. LAMMPS MD simulator, http://lammps.sandia.gov/index.html .
- 12. Y. Mishin, M. J. Mehl, D. A. Papaconstantopoulos, A. F. Voter and J. D. Kress: Phys. Rev. B, 63 (2001) 224106. .Article
- 13. R. M. German: Powder metallurgy and particulate materials processing: the processes, materials, products, properties, and applications, Metal Powder Industries Federation, Princeton, NJ (2005). .
- 14. Y. Mishin and C. Herzig: Mater. Sci. Eng., 260 (1999) 55. .Article
- 15. M. A. Tschopp and D. L. McDowell: Phil. Mag., 87 (2007) 3871..Article
Figure & Data
References
Citations

- Mesoscale modelling of polymer powder densification due to thermal sintering
Amine Bahloul, Issam Doghri, Laurent Adam
Applied Mathematical Modelling.2023; 114: 408. CrossRef - Review of “Integrated Computer-Aided Process Engineering Session in the International Symposium on Innovation in Materials Processing (ISIMP, 26–29 October 2021)”
Hyunjoo Choi, Jungjoon Kim, Pil-Ryung Cha, Hyoung Seop Kim
MATERIALS TRANSACTIONS.2023; 64(10): 2542. CrossRef - Enhancement in electrical conductivity of pastes containing submicron Ag-coated Cu filler with palmitic acid surface modification
Eun Byeol Choi, Jong-Hyun Lee
Applied Surface Science.2017; 415: 67. CrossRef



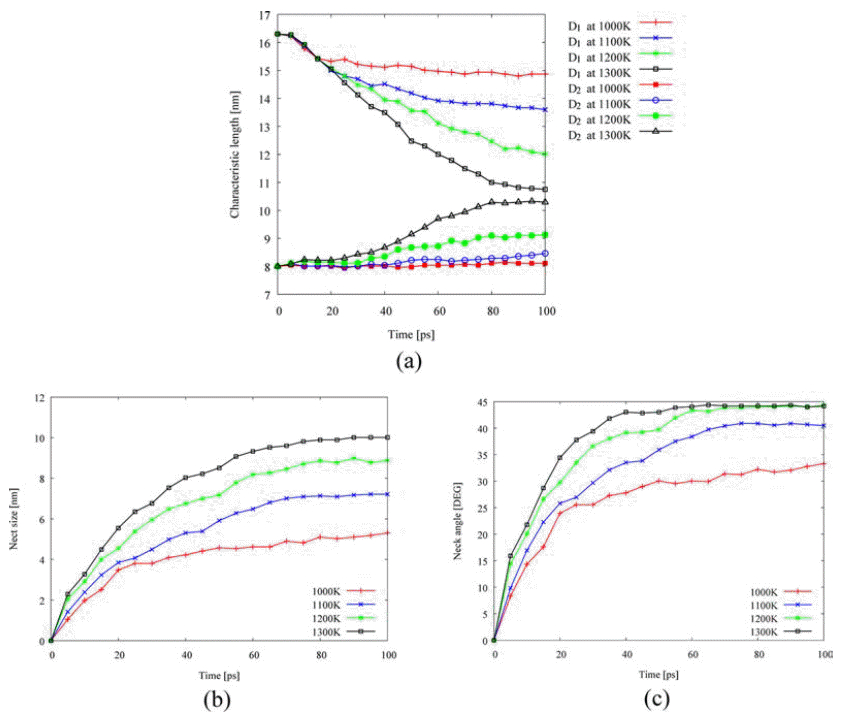



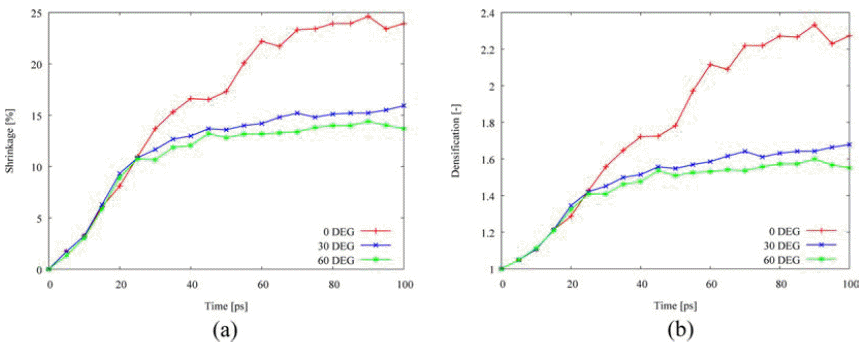
Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
| Sintering mechanism | Activation energy (kJ/mol) | |
|---|---|---|
|
|
||
| Two-particle model | Ref. [13] | |
|
|
||
| Viscous flow or Plastic flow | 63.97 | 197 |
| Evaporation-condensation | 86.91 | 307 |
| Lattice(volume) diffusion | 145.18 | 213 |
| Grain-boundary diffusion | 168.85 | 107 |
| Surface diffusion | 203.70 | 205 |
| Radius | Activation energy (kJ/mol) | ||
|---|---|---|---|
|
|
|||
| Mechanism | 2.896 nm | 3.982 nm | 5.430 nm |
|
|
|||
| Viscous flow or Plastic flow | 62.77 | 63.97 | 63.88 |
| Evaporation-condensation | 85.58 | 86.91 | 88.10 |
| Lattice(volume) diffusion | 136.78 | 145.18 | 149.42 |
| Grain-boundary diffusion | 160.32 | 168.85 | 173.30 |
| Surface diffusion | 188.40 | 203.70 | 210.19 |
| Tilt angle | Activation energy (kJ/mol) | ||
|---|---|---|---|
|
|
|||
| Mechanism | 0° | 30° | 60° |
|
|
|||
| Viscous flow or Plastic flow | 63.97 | 74.65 | 80.85 |
| Evaporation-condensation | 86.91 | 99.50 | 108.84 |
| Lattice(volume) diffusion | 145.18 | 161.20 | 176.19 |
| Grain-boundary diffusion | 168.85 | 186.59 | 204.07 |
| Surface diffusion | 203.70 | 223.21 | 243.44 |
Table 1
Table 2
Table 3
TOP
 KPMI
KPMI

 Cite this Article
Cite this Article